Question

【题目】如图,在四棱锥S-ABCD中,底面ABCD为直角梯形,AD//BC,∠SAD =∠DAB= ,SA=3,SB=5,,,.

(1)求证:AB平面SAD；

(2)求平面SCD与平面SAB所成的锐二面角的余弦值；

(3)点E,F分别为线段BC,SB上的一点,若平面AEF//平面SCD,求三棱锥B-AEF的体积.

Answer 1

【答案】(1) 见解析；(2) ； (3)1

【解析】

（1）通过证明，得线面垂直；

（2）结合第一问结论，建立空间直角坐标系，求出两个平面的法向量，即可得二面角的余弦值；

（3）根据面面平行关系得出点F的位置，即可得到体积.

(1)证明:在中,因为,

所以.

又因为∠DAB=900

所以,

因为

所以平面SAD.

(2)解:因为 AD,,，

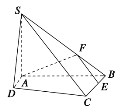
建立如图直角坐标系：

则A(0,0,0)B(0,4,0), C(2,4,0),D(1,0,0),S(0,0,3).

平面SAB的法向量为.

设平面SDC的法向量为

所以有

即,

令，

所以平面SDC的法向量为

所以.

(3)因为平面AEF//平面SCD,

平面AEF平面ABCD=AE,平面SCD平面ABCD=CD,

所以,

平面AEF平面SBC=EF,平面SCD平面SBC=SC,

所以

由,AD//BC

得四边形AEDC为平行四边形.

所以E为BC中点.

又,

所以F为SB中点.

所以F到平面ABE的距离为,

又的面积为2,

所以.