题目内容
【题目】已知数列{an}为等差数列,a1=1,前n项和为Sn,数列{bn}为等比数列,b1>1,公比为2,且b2S3=54,b3+S2=16.
(Ⅰ)求数列{an}与{bn}的通项公式;
(Ⅱ)设数列{cn}满足cn=an+bn,求数列{cn}的前n项和Tn.
【答案】(Ⅰ) an=2n﹣1,
; (Ⅱ)Tn.
n2+3(2n﹣1).
【解析】
(Ⅰ)利用等差数列的前
项和公式和等比数列的通项公式列式解方程组解得
和
，进一步可得
和
；
(Ⅱ)利用等差数列与等比数列的前项和公式分组求和可得.
(Ⅰ)∵数列{an}为等差数列,a1=1,前n项和为Sn,数列{bn}为等比数列,
b1>1,公比为2,且b2S3=54,b3+S2=16.
∴
,
解得b1=3,d=2,
∴an=2n﹣1,;
(Ⅱ)∵cn=an+bn=(2n﹣1)+32n﹣1.
∴Tn=c1+c2+…+cn=[1+3+…+(2n﹣1)]+3(1+2+22+…+2n﹣1)
n2+3(2n﹣1).
特高级教师点拨系列答案
【题目】在新的劳动合同法出台后，某公司实行了年薪制工资结构改革．该公司从2008年起，每人的工资由三个项目构成，并按下表规定实施：
项目 | 金额[元/（人年）] | 性质与计算方法 |
基础工资 | 2007年基础工资为20000元 | 考虑到物价因素，决定从2008年 起每年递增10%（与工龄无关） |
房屋补贴 | 800 | 按职工到公司年限计算，每年递增800元 |
医疗费 | 3200 | 固定不变 |
如果该公司今年有5位职工，计划从明年起每年新招5名职工．
（1）若今年算第一年，将第n年该公司付给职工工资总额y（万元）表示成年限n的函数；
（2）若公司每年发给职工工资总额中，房屋补贴和医疗费的总和总不会超过基础工资总额的p%，求p的最小值．
【题目】某工厂生产一批零件，为了解这批零件的质量状况，检验员从这批产品中随机抽取了100件作为样本进行检测，将它们的重量（单位：g）作为质量指标值．由检测结果得到如下频率分布直方图．
分组 | 频数 | 频率 |
| 8 | |
| ||
| ||
| 16 | 0.16 |
| 4 | 0.04 |
合计 | 100 | 1 |
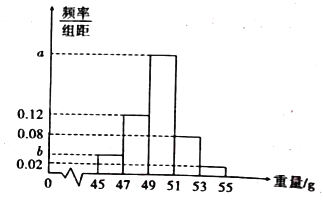
（1）求图中
的值；
（2）根据质量标准规定：零件重量小于47或大于53为不合格品，重量在区间
和
内为合格品，重量在区间
内为优质品．已知每件产品的检测费用为5元，每件不合格品的回收处理费用为20元．以抽检样本重量的频率分布作为该零件重量的概率分布．若这批零件共
件
，现有两种销售方案：方案一：不再检测其他零件，整批零件除对已检测到的不合格品进行回收处理，其余零件均按150元/件售出；方案二：继续对剩余零件的重量进行逐一检测，回收处理所有不合格品，合格品按150元/件售出，优质品按200元/件售出．仅从获得利润大的角度考虑，该生产商应选择哪种方案？请说明理由．
