题目内容
【题目】已知f（x）=log4（4x+1）+kx是偶函数．
（1）求k的值；
（2）判断函数y=f（x）-
x在R上的单调性，并加以证明；
（3）设g（x）=log4（a2x-
a），若函数f（x）与g（x）的图象有且仅有一个交点，求实数a的取值范围．
【答案】（1）k=-
(2)见证明；(3) （1，+∞）∪{-3}
【解析】
（1）由偶函数的定义可得f（-x）=f（x），结合对数函数的运算性质，解方程可得所求值；
（2）函数h（x）=f（x）-x=log4（4x+1）-x在R上递减，运用单调性的定义和对数函数的单调性，即可证明；
（3）由题意可得log4（4x+1）-x=log4（a2x-
a）有且只有一个实根，可化为2x+2-x=a2x-a，即有a=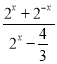
，化为a-1=
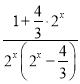，运用换元法和对勾函数的单调性，即可得到所求范围．
（1）f（x）=log4（4x+1）+kx是偶函数，
可得f（-x）=f（x），即log4（4-x+1）-kx=log4（4x+1）+kx，
即有log4
=2kx，可得
，即
由x∈R，可得
；
（2）函数h（x）=f（x）-x=log4（4x+1）-x在R上递减，
理由：设x1＜x2，则h（x1）-h（x2）=log4（4x1+1）-x1-log4（4x2+1）+x2
=log4（4-x1+1）-log4（4-x2+1），
由x1＜x2，可得-x1＞-x2，可得log4（4-x1+1）＞log4（4-x2+1），
则h（x1）＞h（x2），即y=f（x）-x在R上递减；
（3）g（x）=log4（a2x-a），若函数f（x）与g（x）的图象有且仅有一个交点，
即为log4（4x+1）-x=log4（a2x-a）有且只有一个实根，
可化为2x+2-x=a2x-a，
即有a=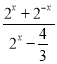，化为a-1=，
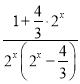可令t=1+2x（t＞1），则2x=
，
则a-1=
=
，
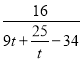由9t+
-34在（1，
）递减，（，+∞）递增，
可得9t+-34的最小值为2
-34=-4，
当a-1=-4时，即a=-3满足两图象只有一个交点；
当t=1时，9t+-34=0，可得a-1＞0时，即a＞1时，两图象只有一个交点，
综上可得a的范围是（1，+∞）∪{-3}．
