题目内容
【题目】如图,在四棱锥P-ABCD中,底面ABCD为菱形,![]() ,点O为AD的中点,
,点O为AD的中点,![]() 且
且![]() .
.
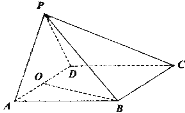
(1)求证:![]() 平面PAD;
平面PAD;
(2)若![]() ,求平面PBC与平面PAD所成二面角的正弦值.
,求平面PBC与平面PAD所成二面角的正弦值.
【答案】(1)见证明;(2)![]()
【解析】
(1)连结OP,BD,先证![]() ,则
,则![]() ,设
,设![]() ,可表示OB,PO,由勾股定理可得
,可表示OB,PO,由勾股定理可得![]() ,从而根据线面垂直的判定定理证明结论;
,从而根据线面垂直的判定定理证明结论;
(2)根据条件证明![]() ,可得OA,OB,OP所在的直线两两互相垂直,故以OA,OB,OP所在直线为x轴,y轴,z轴建立坐标系,由
,可得OA,OB,OP所在的直线两两互相垂直,故以OA,OB,OP所在直线为x轴,y轴,z轴建立坐标系,由![]() 平面PAD,故可以取与
平面PAD,故可以取与![]() 平行的向量
平行的向量![]() 作为平面PAD的法向量,再利用空间向量法求出平面PBC的法向量
作为平面PAD的法向量,再利用空间向量法求出平面PBC的法向量![]() ,从而利用向量的夹角公式求得结果.
,从而利用向量的夹角公式求得结果.
(1)证明:连结OP,BD,因为底面ABCD为菱形,![]() ,
,
故![]() ,又O为AD的中点,故
,又O为AD的中点,故![]() .
.
在![]() 中,
中,![]() ,O为AD的中点,所以
,O为AD的中点,所以![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,
因为![]() ,
,
所以![]() .(也可通过
.(也可通过![]() 来证明
来证明![]() ),
),
又因为![]() ,
,![]() 平面PAD,
平面PAD,![]() 平面PAD,
平面PAD,
所以![]() 平面PAD;
平面PAD;
(2)因为![]() ,
,![]() ,
,
![]() ,
,![]() 平面POB,
平面POB,![]() 平面POB,
平面POB,
所以![]() 平面POB,又
平面POB,又![]() 平面POB,所以
平面POB,所以![]() .
.
由(1)得![]() 平面PAD,又
平面PAD,又![]() 平面PAD,故有
平面PAD,故有![]() ,又由
,又由![]() ,
,
所以OA,OB,OP所在的直线两两互相垂直.
故以O为坐标原点,以OA,OB,OP所在直线为x轴,y轴,z轴如图建系.
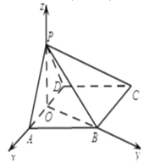
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() ,
,
由(1)知![]() 平面PAD,
平面PAD,
故可以取与![]() 平行的向量
平行的向量![]() 作为平面PAD的法向量.
作为平面PAD的法向量.
设平面PBC的法向量为![]() ,则
,则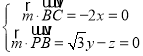 ,
,
令![]() ,所以
,所以![]() .
.
设平面PBC与平面PAD所成二面角为θ,则![]() ,
,
则![]() ,所以平面PBC与平面PAD所成二面角的正弦值为
,所以平面PBC与平面PAD所成二面角的正弦值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】规定投掷飞镖3次为一轮,3次中至少两次投中8环以上的为优秀.现采用随机模拟实验的方法估计某人投掷飞镖的情况:先由计算器产生随机数0或1,用0表示该次投镖未在8环以上,用1表示该次投镖在8环以上;再以每三个随机数作为一组,代表一轮的结果.例如:“101”代表第一次投镖在8环以上,第二次投镖未在8环以上,第三次投镖在8环以上,该结果代表这一轮投镖为优秀:"100”代表第一次投镖在8环以上,第二次和第三次投镖均未在8环以上,该结果代表这一轮投镖为不优秀.经随机模拟实验产生了如下10组随机数,据此估计,该选手投掷飞镖两轮,至少有一轮可以拿到优秀的概率是( )
101 | 111 | 011 | 101 | 010 | 100 | 100 | 011 | 111 | 001 |
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()