题目内容
【题目】已知等比数列![]() 的首项
的首项![]() ,数列
,数列![]() 前
前![]() 项和记为
项和记为![]() ,前
,前![]() 项积记为
项积记为![]() .
.
(1) 若![]() ,求等比数列
,求等比数列![]() 的公比
的公比![]() ;
;
(2) 在(1)的条件下,判断![]() 与
与![]() 的大小;并求
的大小;并求![]() 为何值时,
为何值时,![]() 取得最大值;
取得最大值;
(3) 在(1)的条件下,证明:若数列![]() 中的任意相邻三项按从小到大排列,则总可以使其成等差数列;若所有这些等差数列的公差按从小到大的顺序依次记为
中的任意相邻三项按从小到大排列,则总可以使其成等差数列;若所有这些等差数列的公差按从小到大的顺序依次记为![]() ,则数列
,则数列![]() 为等比数列.
为等比数列.
【答案】(1)![]() ;(2)
;(2)![]() ,当
,当![]() 时,
时,![]() 最大;(3)证明见解析.
最大;(3)证明见解析.
【解析】
(1)![]() ,求
,求![]() 和通项公式;
和通项公式;
(2)根据定义可知![]() ,然后根据公式
,然后根据公式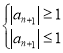 求
求![]() ,即
,即![]() 时
时![]() 的最大值,再根据
的最大值,再根据![]() ,判断
,判断![]() 的最大值;
的最大值;
(3)由(1)可知当![]() 为奇数时,
为奇数时,![]() 中的任意相邻三项由小到大排列是
中的任意相邻三项由小到大排列是![]() ,若成等差数列,可求
,若成等差数列,可求![]() 是否成立,并求公差,当
是否成立,并求公差,当![]() 是偶数时,设
是偶数时,设![]() 中的任意相邻三项按从小到大排列为
中的任意相邻三项按从小到大排列为![]() ,判断是否成等差数列,并求公差,并按定义判断数列
,判断是否成等差数列,并求公差,并按定义判断数列![]() 是否为等比数列
是否为等比数列
(1) ![]() ,解得
,解得![]() ,
,![]() ;
;
(2)![]() .又
.又![]() ,
,
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.![]() 当
当![]() 时,
时,![]() 取得最大值,
取得最大值,
又![]() ,∴
,∴![]() 的最大值是
的最大值是![]() 和
和![]() 中的较大者,
中的较大者,
又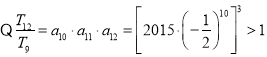 ,
,![]() .因此当
.因此当![]() 时,
时,![]() 最大.
最大.
(3)![]() ,
,![]() 随
随![]() 增大而减小,
增大而减小,![]() 奇数项均正,偶数项均负,
奇数项均正,偶数项均负,
①当![]() 是奇数时,设
是奇数时,设![]() 中的任意相邻三项按从小到大排列为
中的任意相邻三项按从小到大排列为![]() ,
,
则![]() ,
,![]() ,
,
![]() ,因此
,因此![]() 成等差数列,
成等差数列,
公差![]() ;
;
②当![]() 是偶数时,设
是偶数时,设![]() 中的任意相邻三项按从小到大排列为
中的任意相邻三项按从小到大排列为![]() ,
,
则![]() ,
,![]() .
.
∴![]() ,因此
,因此![]() 成等差数列,
成等差数列,
公差![]() ,
,
综上可知,![]() 中的任意相邻三项按从小到大排列,总可以使其成等差数列,
中的任意相邻三项按从小到大排列,总可以使其成等差数列,
且![]() , ∵
, ∵![]() ,∴数列
,∴数列![]() 为等比数列.
为等比数列.

练习册系列答案
相关题目