题目内容
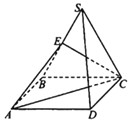
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() 上运动(其中
上运动(其中![]() 不与
不与![]() ,
,![]() 重合,
重合,![]() 不与
不与![]() ,
,![]() 重合),且
重合),且![]() ,沿
,沿![]() 将
将![]() 折起,得到三棱锥
折起,得到三棱锥![]() ,则三棱锥
,则三棱锥![]() 体积的最大值为______;当三棱锥
体积的最大值为______;当三棱锥![]() 体积最大时,其外接球的半径
体积最大时,其外接球的半径![]() ______.
______.
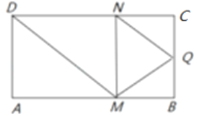
【答案】1 ![]()
【解析】
易知当平面![]() 平面
平面![]() 时,三棱锥
时,三棱锥![]() 体积最大,此时
体积最大,此时![]() 平面
平面![]() .DN为几何体的高,设
.DN为几何体的高,设![]() ,则
,则![]() ,且
,且![]() ,再由V三棱锥D-MNQ
,再由V三棱锥D-MNQ![]() 求解,当三棱锥
求解,当三棱锥![]() 体积最大时,三棱锥
体积最大时,三棱锥![]() 是正三棱柱的一部分,则三棱柱
是正三棱柱的一部分,则三棱柱![]() 的外接球即是三棱锥
的外接球即是三棱锥![]() 的外接球,设点
的外接球,设点![]() ,
,![]() 分别是上下底面正三角形的中心,则线段
分别是上下底面正三角形的中心,则线段![]() 的中点即是三棱柱
的中点即是三棱柱![]() 的外接球的球心
的外接球的球心![]() 求解.
求解.
当平面![]() 平面
平面![]() 时,三棱锥
时,三棱锥![]() 体积最大,
体积最大,
这时![]() 平面
平面![]() .
.
设![]() ,则
,则![]() ,且
,且![]() ,
,
则V三棱锥D-MNQ![]() ,
,
当![]() 时,三棱锥
时,三棱锥![]() 体积最大,且
体积最大,且![]() .此时
.此时![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴当三棱锥![]() 体积最大时,三棱锥
体积最大时,三棱锥![]() 是正三棱柱的一部分,
是正三棱柱的一部分,
如图所示:
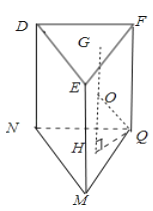
则三棱柱![]() 的外接球即是三棱锥
的外接球即是三棱锥![]() 的外接球,
的外接球,
设点![]() ,
,![]() 分别是上下底面正三角形的中心,
分别是上下底面正三角形的中心,
∴线段![]() 的中点即是三棱柱
的中点即是三棱柱![]() 的外接球的球心
的外接球的球心![]() ,
,
∴![]() ,
,
又∵![]() 是边长为2的等边三角形,
是边长为2的等边三角形,
∴![]() ,
,
∴三棱柱![]() 的外接球的半径
的外接球的半径![]() .
.
故答案为:1;![]() .
.

练习册系列答案
相关题目