题目内容
【题目】设函数![]() .
.
(1)若当![]() 时,
时,![]() 取得极值,求
取得极值,求![]() 的值,并求
的值,并求![]() 的单调区间.
的单调区间.
(2)若![]() 存在两个极值点
存在两个极值点![]() ,求
,求![]() 的取值范围,并证明:
的取值范围,并证明:![]() .
.
【答案】(1)![]() ,
,![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() . (2)
. (2)![]() ,证明见解析
,证明见解析
【解析】
(1)求导数![]() ,由题意可知
,由题意可知![]() 为方程
为方程![]() 的根,求解
的根,求解![]() 值,即可.再令导数
值,即可.再令导数![]() ,
,![]() ,分别求解单调增区间与单调减区间,即可.
,分别求解单调增区间与单调减区间,即可.
(2)函数![]() 存在两个极值点,等价于方程
存在两个极值点,等价于方程![]() 即
即![]() 在
在![]() 上有两个不等实根,则
上有两个不等实根,则![]() ,即可.
,即可. ![]() 变形整理为
变形整理为![]() ;若证明不等式
;若证明不等式![]() ,则需证明
,则需证明![]() ,由
,由![]() 变形为
变形为![]() ,不妨设
,不妨设![]() ,即证
,即证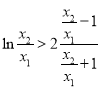 ,令
,令![]() ,则
,则![]() ,求函数
,求函数![]() 的取值范围,即可证明.
的取值范围,即可证明.
(1)![]()
![]() 时,
时,![]() 取得极值.
取得极值.
![]() .
.
![]()
解![]() 得
得![]() 或
或![]()
解![]() 得
得![]()
![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
(2)![]()
![]() 存在两个极值点
存在两个极值点
![]() 方程
方程![]() 即
即![]() 在
在![]() 上有两个不等实根.
上有两个不等实根.
![]() ,
,![]()
![]() .
.
![]()
![]()
![]() 所证不等式
所证不等式![]() 等价于
等价于![]()
即![]()
不妨设![]() ,即证
,即证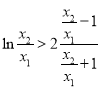
令![]() ,
,![]()
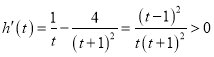 ,
,![]() 在
在![]() 上递增.
上递增.
![]()
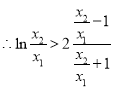 成立.
成立.
![]() 成立.
成立.

练习册系列答案
相关题目
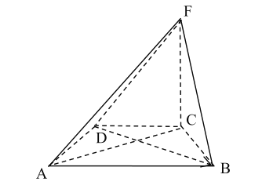
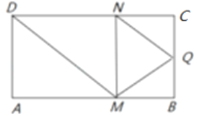
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() 上运动(其中
上运动(其中![]() 不与
不与![]() ,
,![]() 重合,
重合,![]() 不与
不与![]() ,
,![]() 重合),且
重合),且![]() ,沿
,沿![]() 将
将![]() 折起,得到三棱锥
折起,得到三棱锥![]() ,则三棱锥
,则三棱锥![]() 体积的最大值为______;当三棱锥
体积的最大值为______;当三棱锥![]() 体积最大时,其外接球的半径
体积最大时,其外接球的半径![]() ______.
______.
【题目】某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
|
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图:

(2)估计该家庭使用节水龙头后,日用水量小于0.35 m3的概率;
(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)