题目内容
【题目】已知函数![]() .
.
(1)求证:![]() ;
;
(2)用![]() 表示
表示![]() 中的最大值,记
中的最大值,记![]() ,讨论函数
,讨论函数![]() 零点的个数.
零点的个数.
【答案】(1)见解析,(2)见解析
【解析】
(1) 设![]() 求出函数的最小值即可;
求出函数的最小值即可;
(2) 对x和a的范围进行讨论,得出f(x),g(x)在(0,+∞)上的单调性,利用单调性及最值判断f(x),g(x)的零点个数,从而得出h(x)的零点个数.
(1)证明:设![]() ,定义域为
,定义域为![]() ,
,
则![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
故![]() 在
在![]() 内是减函数,在
内是减函数,在![]() 内是增函数,
内是增函数,
所以![]() 是
是![]() 的极小值点,也是
的极小值点,也是![]() 的最小值点,
的最小值点,
所以![]() ,所以
,所以![]()
(2)解:函数![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 内是减函数,在
内是减函数,在![]() 内是增函数,
内是增函数,
所以![]() 是
是![]() 的极小值点,也是
的极小值点,也是![]() 的最小值点,
的最小值点,
即![]()
若![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
所以![]() ,于是
,于是![]() 只有一个零点
只有一个零点![]() .
.
当![]() ,则当
,则当![]() 时,
时,![]() ,此时
,此时![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,此时
,此时![]()
所以![]() 没有零点.
没有零点.
当![]() ,则当
,则当![]() 时,根据(1)可知,
时,根据(1)可知,![]()
而![]() ,所以
,所以![]()
又因为![]() ,所以
,所以![]() 在
在![]() 上有一个零点
上有一个零点![]() ,
,
从而一定存在![]() ,使得
,使得![]() ,
,
即![]() ,所以
,所以![]() .
.
当![]() 时,
时,![]() ,
,
所以![]() ,从而
,从而![]() ,
,
于是![]() 有两个零点
有两个零点![]() 和1.
和1.
故当![]() 时,
时,![]() 有两个零点.
有两个零点.
综上,当![]() 时,
时,![]() 有一个零点,当
有一个零点,当![]() 时,
时,![]() 没有零点,当
没有零点,当![]() 时,
时,![]() 有两个零点.
有两个零点.

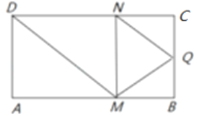
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() 上运动(其中
上运动(其中![]() 不与
不与![]() ,
,![]() 重合,
重合,![]() 不与
不与![]() ,
,![]() 重合),且
重合),且![]() ,沿
,沿![]() 将
将![]() 折起,得到三棱锥
折起,得到三棱锥![]() ,则三棱锥
,则三棱锥![]() 体积的最大值为______;当三棱锥
体积的最大值为______;当三棱锥![]() 体积最大时,其外接球的半径
体积最大时,其外接球的半径![]() ______.
______.
【题目】某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
|
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图:

(2)估计该家庭使用节水龙头后,日用水量小于0.35 m3的概率;
(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)
【题目】某城市对一项惠民市政工程满意程度(分值:![]() 分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):
分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):

现用分层抽样的方法从所有参与网上投票的市民中随机抽取![]() 位市民召开座谈会,其中满意程度在
位市民召开座谈会,其中满意程度在![]() 的有5人.
的有5人.
(1)求![]() 的值,并填写下表(2000位参与投票分数和人数分布统计);
的值,并填写下表(2000位参与投票分数和人数分布统计);
满意程度(分数) |
|
|
|
|
|
人数 |
(2)求市民投票满意程度的平均分(各分数段取中点值);
(3)若满意程度在![]() 的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.
的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.