题目内容
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为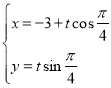 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知点![]() 是曲线
是曲线![]() 上的任意一点,当点
上的任意一点,当点![]() 到直线
到直线![]() 的距离最大时,求经过点
的距离最大时,求经过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() ,
,![]() (Ⅱ)
(Ⅱ)![]()
【解析】
(Ⅰ)消去直线的参数即可得到直线![]() 的普通方程,利用极坐标和直线坐标互化的公式可得到曲线C的直角坐标方程. (Ⅱ)设直线
的普通方程,利用极坐标和直线坐标互化的公式可得到曲线C的直角坐标方程. (Ⅱ)设直线![]() 的方程为
的方程为![]() ,得到当点
,得到当点![]() 到直线
到直线![]() 的距离最大时,为经过圆心与直线
的距离最大时,为经过圆心与直线![]() 垂直的直线与圆的交点,利用点到直线的距离可求出
垂直的直线与圆的交点,利用点到直线的距离可求出![]() 的值.
的值.
解:(Ⅰ)直线![]() 的参数方程为
的参数方程为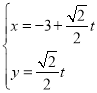 (
(![]() 为参数),消去
为参数),消去![]() 即
即![]() .
.
因为![]() ,
,![]() ,所以极坐标方程
,所以极坐标方程![]() 化直角坐标方程为:
化直角坐标方程为:![]() .
.
(Ⅱ)曲线![]() 的方程为
的方程为![]() ,即
,即![]() ,圆心
,圆心![]() ,圆心到直线的距离为
,圆心到直线的距离为![]()
点![]() 到直线
到直线![]() 的距离最大时,
的距离最大时,![]() 为过圆心且与直线
为过圆心且与直线![]() 垂直的直线与圆的交点,此时,点
垂直的直线与圆的交点,此时,点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
设直线![]() :
:![]() ,则
,则![]() ,即
,即![]() (舍)或
(舍)或![]() .
.
所以直线![]() 的方程为
的方程为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
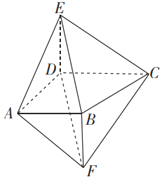
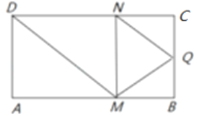
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() 上运动(其中
上运动(其中![]() 不与
不与![]() ,
,![]() 重合,
重合,![]() 不与
不与![]() ,
,![]() 重合),且
重合),且![]() ,沿
,沿![]() 将
将![]() 折起,得到三棱锥
折起,得到三棱锥![]() ,则三棱锥
,则三棱锥![]() 体积的最大值为______;当三棱锥
体积的最大值为______;当三棱锥![]() 体积最大时,其外接球的半径
体积最大时,其外接球的半径![]() ______.
______.
【题目】某城市对一项惠民市政工程满意程度(分值:![]() 分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):
分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):

现用分层抽样的方法从所有参与网上投票的市民中随机抽取![]() 位市民召开座谈会,其中满意程度在
位市民召开座谈会,其中满意程度在![]() 的有5人.
的有5人.
(1)求![]() 的值,并填写下表(2000位参与投票分数和人数分布统计);
的值,并填写下表(2000位参与投票分数和人数分布统计);
满意程度(分数) |
|
|
|
|
|
人数 |
(2)求市民投票满意程度的平均分(各分数段取中点值);
(3)若满意程度在![]() 的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.
的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.