题目内容
已知命题p:?x∈R,使sinx-cosx=
,命题q:集合{x|x2-2x+1=0,x∈R}有2个子集,下列结论:
(1)命题“p∧q”是真命题;
(2)命题“p∧(¬q)”是假命题;
(3)命题“(¬p)∨(¬q)”是真命题.
正确的个数是( )
| 3 |
(1)命题“p∧q”是真命题;
(2)命题“p∧(¬q)”是假命题;
(3)命题“(¬p)∨(¬q)”是真命题.
正确的个数是( )
| A.0 | B.1 | C.2 | D.3 |
∵sinx-cosx=
sin(x-
)∈[-
,
]
∴sinx-cosx=
∉[-
,
]
∴命题p是假命题
又∵集合{x|x2-2x+1=0,x∈R}={1},
那么{1}的子集有两个:{1}、φ,
∴命题q是真命题
由复合命题判定真假可知.
(1)命题“p∧q”是真命题,错误
(2)命题“p∧(¬q)”是假命题,正确
(3)命题“(△¬p)∨(¬q)”是真命题,正确
故选C
| 2 |
| π |
| 4 |
| 2 |
| 2 |
∴sinx-cosx=
| 3 |
| 2 |
| 2 |
∴命题p是假命题
又∵集合{x|x2-2x+1=0,x∈R}={1},
那么{1}的子集有两个:{1}、φ,
∴命题q是真命题
由复合命题判定真假可知.
(1)命题“p∧q”是真命题,错误
(2)命题“p∧(¬q)”是假命题,正确
(3)命题“(△¬p)∨(¬q)”是真命题,正确
故选C

练习册系列答案
相关题目
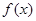 在
在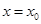 处导数存在,若
处导数存在,若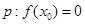 ;
;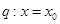 是
是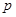 是
是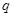 的充分必要条件
的充分必要条件