题目内容
已知m∈R,设命题p:关于x的不等式x2+mx+2m<0有解;命题q:若a>b,则am>bm.若命题“¬p”与“p∨q”都为真命题,求m的取值范围.
∵命题p:关于x的不等式x2+mx+2m<0有解
∴若命题p为真命题,则由△=m2-8m>0得,
∴m>8或m<0
∵命题q:若a>b,则am>bm.
∴命题q为真命题,
∴m>0
∵“¬p”与“p∨q”都为真命题
∴命题p为假命题,命题q为真命题
∴由
,得0<m≤8
∴m的取值范围为0<m≤8
∴若命题p为真命题,则由△=m2-8m>0得,
∴m>8或m<0
∵命题q:若a>b,则am>bm.
∴命题q为真命题,
∴m>0
∵“¬p”与“p∨q”都为真命题
∴命题p为假命题,命题q为真命题
∴由
|
∴m的取值范围为0<m≤8

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
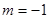 是直线
是直线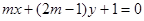 和直线
和直线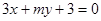 垂直的( )
垂直的( )