题目内容
已知命题p:对于m∈[-1,1],不等式a2-5a-3≥
恒成立;命题q:不等式x2+ax+2<0有解,若p∨q为真,且p∧q为假,求a的取值范围.
| m2+8 |
若命题p:对于m∈[-1,1],不等式a2-5a-3≥
恒成立;
由于(
)max=3,∴a2-5a-3≥3,解得a≥6或a≤-1.
若命题q:不等式x2+ax+2<0有解,则△=a2-8≥0,解得a≥2
或a≤-2
.
若p∨q为真,且p∧q为假,则p与q一真一假.
当p真q假时,
,解得-2
<a≤-1,此时a∈(-2
,-1].
当q真p假时,
,解得2
≤a<6,此时a∈[2
,6).
综上可知:a的取值范围是(-2
,-1]∪[2
,6).
| m2+8 |
由于(
| m2+8 |
若命题q:不等式x2+ax+2<0有解,则△=a2-8≥0,解得a≥2
| 2 |
| 2 |
若p∨q为真,且p∧q为假,则p与q一真一假.
当p真q假时,
|
| 2 |
| 2 |
当q真p假时,
|
| 2 |
| 2 |
综上可知:a的取值范围是(-2
| 2 |
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
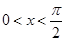 ,则“
,则“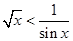 ”是“
”是“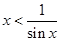 ”的( )
”的( )