题目内容
1.函数y=$|tan(-2x-\frac{π}{6})|$+3图象的对称轴方程为x=$\frac{kπ}{4}$-$\frac{π}{12}$,k∈Z,周期为π,单调递减区间为($\frac{kπ}{2}$-$\frac{π}{3}$,$\frac{kπ}{2}$-$\frac{π}{12}$],k∈Z,.分析 根据正切函数的图象和性质进行求解即可.
解答 解:y=$|tan(-2x-\frac{π}{6})|$+3=|tan(2x+$\frac{π}{6}$)|+3,
由2x+$\frac{π}{6}$=$\frac{kπ}{2}$,即x=$\frac{kπ}{4}$-$\frac{π}{12}$,k∈Z,
即函数的对称轴方程为x=$\frac{kπ}{4}$-$\frac{π}{12}$,k∈Z,
函数的周期T=$\frac{π}{2}$,
由kπ-$\frac{π}{2}$<2x+$\frac{π}{6}$≤kπ,k∈Z得
$\frac{kπ}{2}$-$\frac{π}{3}$<x≤$\frac{kπ}{2}$-$\frac{π}{12}$,k∈Z,
即函数的单调递减区间为($\frac{kπ}{2}$-$\frac{π}{3}$,$\frac{kπ}{2}$-$\frac{π}{12}$],k∈Z,
故答案为:x=$\frac{kπ}{4}$-$\frac{π}{12}$,k∈Z,π,($\frac{kπ}{2}$-$\frac{π}{3}$,$\frac{kπ}{2}$-$\frac{π}{12}$],k∈Z,
点评 本题主要考查正切函数的对称轴,周期以及函数单调性的求解,利用正切函数的图象和性质是解决本题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
11.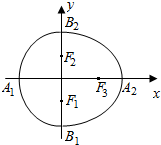 我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x<0)合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是边长为1的等边三角形,则a,b的值分别为( )
我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x<0)合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是边长为1的等边三角形,则a,b的值分别为( )
 我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x<0)合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是边长为1的等边三角形,则a,b的值分别为( )
我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x<0)合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是边长为1的等边三角形,则a,b的值分别为( )| A. | 5,4 | B. | $\sqrt{3}$,1 | C. | 5,3 | D. | $\frac{\sqrt{7}}{2}$,1 |
6.已知函数f(x)=x|x|,则不等式f(x)+f(x2-2)>0的解集为( )
| A. | (-2,1) | B. | (-∞,-2)∪(1,+∞) | C. | (-∞,-1)∪(2,+∞) | D. | (-1,2) |
13.已知O是坐标原点,F是椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的一个焦点,过F且与x轴垂直的直线与椭圆交于M,N两点,则cos∠MON的值为( )
| A. | $\frac{5}{13}$ | B. | -$\frac{5}{13}$ | C. | $\frac{2\sqrt{13}}{13}$ | D. | -$\frac{2\sqrt{13}}{13}$ |