题目内容
在正方体ABCD—A1B1C1D1中,M、N、P、Q分别是棱AB、BC、CD、CC1的中点,直线MN与PQ所成的度数是 ( )
A.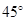 B.
B.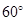 C.
C.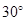 D.
D.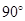
B.
解析试题分析:连接DC1,A 1C1,因为M、N、P、Q分别是棱AB、BC、CD、CC1的中点,
所以MN// A 1C1,PQ// DC1,MN与PQ所成的度数等于A 1C1, DC1所成角的度数为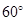 ,
,
故选B。
考点:本题主要考查正方体的几何特征,异面直线所成的角。
点评:简单题,空间问题往往要转化成平面问题,特别是角,转化成在同一四边形、三角形内。

练习册系列答案
相关题目
平面 和直线
和直线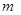 ,给出条件:①
,给出条件:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .为使
.为使 ,应选择下面四个选项中的条件( )
,应选择下面四个选项中的条件( )
| A.①⑤ | B.①④ | C.②⑤ | D.③⑤ |
已知直线 ,平面
,平面 ,且
,且 ,给出四个命题: ①若
,给出四个命题: ①若 ∥
∥ ,则
,则 ;②若
;②若 ,则
,则 ∥
∥ ;③若
;③若 ,则
,则 ∥m;④若
∥m;④若 ∥m,则
∥m,则 .其中真命题的个数是
.其中真命题的个数是
| A.4 | B.3 | C.2 | D.1 |
在三棱锥 中,
中, ,
, 是等腰直角三角形,
是等腰直角三角形,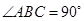 ,
, 为
为 中点. 则
中点. 则 与平面
与平面 所成的角等于( )
所成的角等于( )
A. | B. | C. | D. |
从正方体的八个顶点中任取四个点连线,在能构成的一对异面直线中,其所成的角的度数不可能是
| A.30° | B.45° | C.60° | D.90° |
已知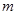 、
、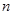 为两条不同的直线,
为两条不同的直线,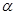 、
、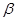 为两个不同的平面,则下列推理中正确的是( )
为两个不同的平面,则下列推理中正确的是( )
A.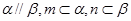 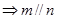 | B.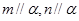 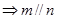 |
C.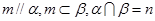 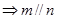 | D.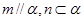 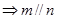 |
 的侧棱与底面边长都相等,
的侧棱与底面边长都相等,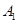 在底面
在底面 上的射影为
上的射影为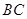 的中点D,则异面直线AD与
的中点D,则异面直线AD与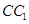 所成的角的余弦值为( )
所成的角的余弦值为( )

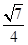
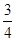
 ,
, ,D为四面体OABC外一点.给出下列命题:①不存在点D,使四面体ABCD有三个面是直角三角形;②不存在点D,使四面体ABCD是正三棱锥;③存在点D,使CD与AB垂直并相等;④存在无数个点D,使点O在四面体ABCD的外接球面上.则其中正确命题的序号是( )
,D为四面体OABC外一点.给出下列命题:①不存在点D,使四面体ABCD有三个面是直角三角形;②不存在点D,使四面体ABCD是正三棱锥;③存在点D,使CD与AB垂直并相等;④存在无数个点D,使点O在四面体ABCD的外接球面上.则其中正确命题的序号是( )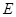 是
是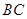 的中点,P点在侧面△SCD内及其边界上运动,并且总是保持
的中点,P点在侧面△SCD内及其边界上运动,并且总是保持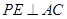 .则动点
.则动点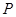 的轨迹与△
的轨迹与△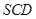 组成的相关图形最有可有是图中的( )
组成的相关图形最有可有是图中的( )