题目内容
已知圆C的方程为x2+y2-10x+21=0,若直线y=kx-3上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是______.
∵圆C的方程为x2+y2-10x+21=0,整理得:(x-5)2+y2=4,即圆C是以(5,0)为圆心,2为半径的圆;
又直线y=kx-3上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,
∴只需圆C′:(x-5)2+y2=9与直线y=kx-3有公共点即可.
设圆心C(5,0)到直线y=kx-3的距离为d,则d=
≤3,
解得0≤k≤
.
∴k的最大值是
.
故答案为:
又直线y=kx-3上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,
∴只需圆C′:(x-5)2+y2=9与直线y=kx-3有公共点即可.
设圆心C(5,0)到直线y=kx-3的距离为d,则d=
| |5k-3| | ||
|
解得0≤k≤
| 15 |
| 8 |
∴k的最大值是
| 15 |
| 8 |
故答案为:
| 15 |
| 8 |

练习册系列答案
相关题目
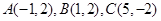 ,若分别以
,若分别以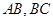 为弦作两外切的圆
为弦作两外切的圆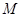 和圆
和圆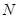 ,且两圆半径相等,则圆的半径为 .
,且两圆半径相等,则圆的半径为 .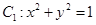 与圆
与圆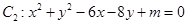 ,则
,则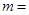 ( )
( )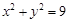 与圆
与圆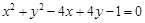 关于直线
关于直线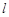 对称,则
对称,则