题目内容
已知一条直线l经过点P(2,1),且与圆x2+y2=10相交,截得的弦长为a.
(Ⅰ)若a=2
,求出直线l的方程;
(Ⅱ)若a=6,求出直线l的方程;
(Ⅲ)求a的取值范围.
(Ⅰ)若a=2
| 6 |
(Ⅱ)若a=6,求出直线l的方程;
(Ⅲ)求a的取值范围.
(Ⅰ)因为圆的圆心坐标(0,0),半径为:
,
设直线的斜率为k,所以直线方程为:y-1=k(x-2),即kx-y-2k+1=0
若a=2
,由垂径定理可得,(
)2=10-(
)2,
解得k=-
,所求直线l的方程为:3x+4y+10=0;
当直线的斜率不存在时直线的方程为:x=2,
故所求直线方程为:3x+4y+10=0或x=2
(Ⅱ)设直线的斜率为k,所以直线方程为:y-1=k(x-2),即kx-y-2k+1=0
若a=6,由垂径定理可得,(
)2=10-32,
解得k=
,或k=0,
所求直线l的方程为:4x-5y-3=0;或y=1.
(Ⅲ)因为点(2,1)在圆内,所以a的最大值为圆的直径:2
,
当直线与OP垂直时,a的值最小,
OP=
=
,所求a的值为:2
=2
.
所以a的范围是:[2
,
].
| 10 |
设直线的斜率为k,所以直线方程为:y-1=k(x-2),即kx-y-2k+1=0
若a=2
| 6 |
| |1-2k| | ||
|
| 6 |
解得k=-
| 3 |
| 4 |
当直线的斜率不存在时直线的方程为:x=2,
故所求直线方程为:3x+4y+10=0或x=2
(Ⅱ)设直线的斜率为k,所以直线方程为:y-1=k(x-2),即kx-y-2k+1=0
若a=6,由垂径定理可得,(
| |1-2k| | ||
|
解得k=
| 4 |
| 5 |
所求直线l的方程为:4x-5y-3=0;或y=1.
(Ⅲ)因为点(2,1)在圆内,所以a的最大值为圆的直径:2
| 10 |
当直线与OP垂直时,a的值最小,
OP=
| 22+12 |
| 5 |
(
|
| 5 |
所以a的范围是:[2
| 5 |
| 10 |

练习册系列答案
相关题目
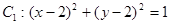 和圆
和圆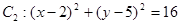 的位置关系为 .
的位置关系为 .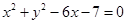 与抛物线
与抛物线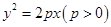 的准线相切,则p的值为________.
的准线相切,则p的值为________.