题目内容
圆x2+y2+2x-6y-15=0与直线(1+3m)x+(3-2m)y+4m-17=0的交点个数是______.
圆x2+y2+2x-6y-15=0化为(x+1)2+(y-3)2=52,圆心坐标(-1,3),半径为5.
直线(1+3m)x+(3-2m)y+4m-17=0化为(x+3y-17)+m(3x-2y+4)=0,
直线恒过
的交点,解方程组可得
,交点坐标(2,5),
交点与圆心的距离为
=
<5.
∴(2,5)在圆的内部,∴直线与圆恒有两个交点.
故答案为:2.
直线(1+3m)x+(3-2m)y+4m-17=0化为(x+3y-17)+m(3x-2y+4)=0,
直线恒过
|
|
交点与圆心的距离为
| (2+1)2+(5-3)2 |
| 13 |
∴(2,5)在圆的内部,∴直线与圆恒有两个交点.
故答案为:2.

练习册系列答案
相关题目
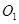 :
: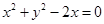 和圆
和圆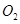 :
: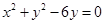 的位置关系( )
的位置关系( )