题目内容
设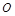 为正方形
为正方形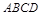 的中心,四边形
的中心,四边形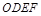 是平行四边形,且平面
是平行四边形,且平面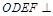 平面
平面 ,若
,若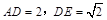 .
.
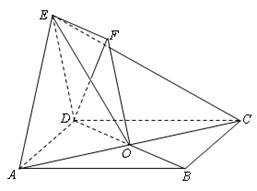
(1)求证: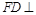 平面
平面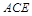 .
.
(2)线段 上是否存在一点
上是否存在一点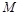 ,使
,使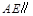 平面
平面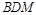 ?若存在,求
?若存在,求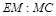 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 为正方形
为正方形 的中心,四边形
的中心,四边形 是平行四边形,且平面
是平行四边形,且平面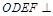 平面
平面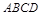 ,若
,若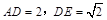 .
.
(1)求证:
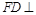 平面
平面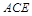 .
.(2)线段
 上是否存在一点
上是否存在一点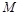 ,使
,使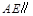 平面
平面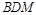 ?若存在,求
?若存在,求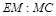 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(1)要证明线面垂直,则可以根据线线垂直,结合判定定理来得到。(2)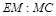 的值为1
的值为1
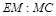 的值为1
的值为1试题分析:解:(1)在正方形
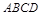 中,
中,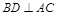 .
.∵
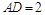 ,∴
,∴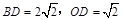 .
.∵
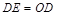 ,∴平行四边形
,∴平行四边形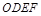 为菱形,∴
为菱形,∴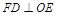 .
.又∵平面
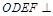 平面
平面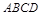 ,∴
,∴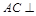 平面
平面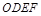 ,∴
,∴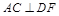 ,
,而
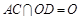 ,∴
,∴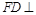 平面
平面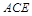 .
. (2)存在线段
 的中点
的中点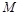 ,使
,使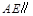 平面
平面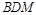 .
.若
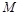 是线段
是线段 的中点,
的中点,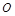 为
为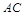 中点,∴
中点,∴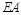 ∥
∥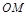 .
.∵
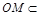 平面
平面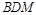 ,
,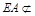 平面
平面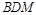 ,∴
,∴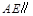 平面
平面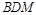 ,
,此时
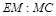 的值为1.
的值为1. 点评:主要是考查了线面的位置关系的运用,属于基础题。

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
 中,
中, ,
, 是
是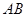 的中点.
的中点. 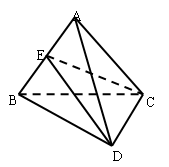
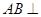 平面CDE;
平面CDE;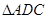 的重心,试在线段AE上确定一点F,使得GF//平面CDE.
的重心,试在线段AE上确定一点F,使得GF//平面CDE.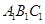 中,底面
中,底面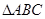 为正三角形,
为正三角形,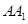
 平面ABC,
平面ABC,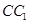 的中点,M是线段
的中点,M是线段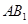 上的动点。
上的动点。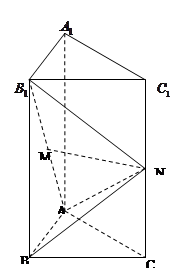
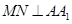 ,请给出证明;
,请给出证明;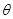 ,求
,求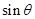 的最大值。
的最大值。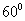 的二面角
的二面角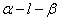 ,点A
,点A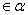 ,
,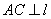 ,C为垂足,
,C为垂足,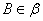 ,BD
,BD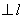 ,D为垂足,若AC=BD=DC=1则AB与
,D为垂足,若AC=BD=DC=1则AB与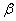 面所成角的正弦值为__________
面所成角的正弦值为__________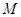 ,
,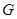 分别是
分别是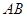 ,
,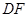 的中点.
的中点.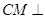 平面
平面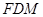 ;
;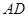 上(含
上(含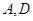 端点)确定一点
端点)确定一点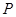 ,使得
,使得 ∥平面
∥平面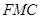 ,并给出证明.
,并给出证明.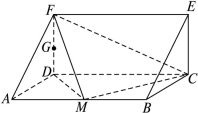
 ,则这个二面角的大小为( )
,则这个二面角的大小为( )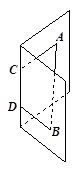




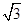 ,BC=1,E为线段DC上一动点,现将
,BC=1,E为线段DC上一动点,现将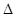 AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为 ( )
AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为 ( ) 
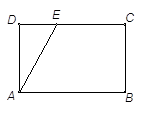
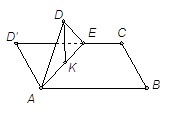
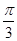
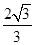
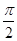
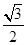
 中,
中, 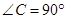 ,
,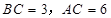 .D、E分别是
.D、E分别是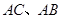 上的点,且
上的点,且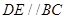 .将
.将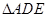 沿
沿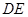 折起到
折起到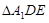 的位置,使
的位置,使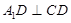 ,如图2.
,如图2.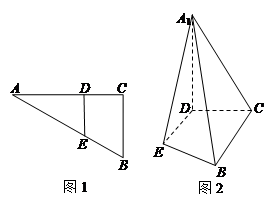
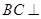 平面
平面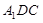 ;
;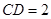 ,求
,求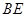 与平面
与平面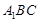 所成角的正弦值;
所成角的正弦值; 的底面
的底面 为一直角梯形,其中
为一直角梯形,其中 ,
,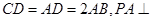 底面
底面 是
是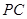 的中点.
的中点.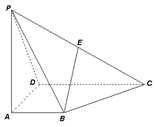
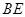 //平面
//平面 ;
; 平面
平面 ,求平面
,求平面 与平面
与平面 夹角的余弦值.
夹角的余弦值.