题目内容
如图,在长方形ABCD中,AB=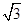 ,BC=1,E为线段DC上一动点,现将
,BC=1,E为线段DC上一动点,现将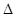 AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为 ( )
AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为 ( )

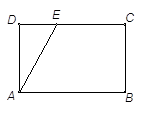
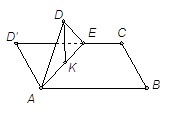
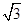 ,BC=1,E为线段DC上一动点,现将
,BC=1,E为线段DC上一动点,现将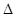 AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为 ( )
AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为 ( ) 
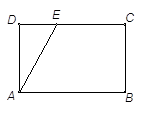
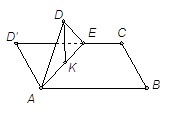
A.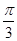 | B.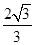 | C.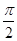 | D.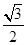 |
A
试题分析:根据△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,可知D′K⊥AE,所以K的轨迹是以AD′为直径的一段圆弧D′K,求出圆心角∠D′OK,即可求得K所形成轨迹的长度.
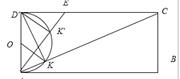
解:由题意,D′K⊥AE,所以K的轨迹是以AD′为直径的一段圆弧D′K,设AD′的中点为O,,∵长方形ABCD′中,AB=
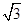 ,BC=1,∴∠D′AC=60°∴∠D′OK=120°=
,BC=1,∴∠D′AC=60°∴∠D′OK=120°=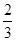 π,∴K所形成轨迹的长度为
π,∴K所形成轨迹的长度为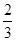 π×
π×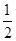 =
=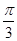 故选A.
故选A.点评:本题以平面图形的翻折为载体,考查立体几何中的轨迹问题,考查弧长公式的运用,解题的关键是利用D′K⊥AE,从而可知K的轨迹是以AD′为直径的一段圆弧D′K

练习册系列答案
相关题目
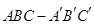 ,
,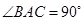 ,
,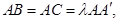 点M,N分别为
点M,N分别为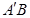 和
和 的中点.
的中点.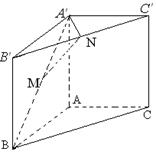
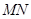 ∥平面
∥平面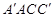 ;
;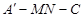 A为直二面角,求
A为直二面角,求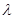 的值.
的值.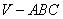 底面为正三角形,侧面
底面为正三角形,侧面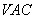 与底面垂直且
与底面垂直且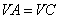 ,已知其主视图的面积为
,已知其主视图的面积为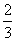 ,则其左视图的面积为
,则其左视图的面积为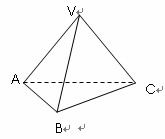
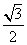

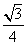
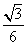
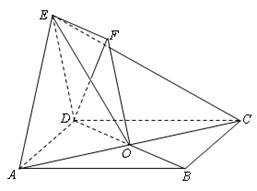
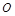 为正方形
为正方形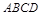 的中心,四边形
的中心,四边形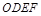 是平行四边形,且平面
是平行四边形,且平面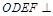 平面
平面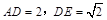 .
.
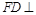 平面
平面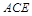 .
. 上是否存在一点
上是否存在一点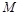 ,使
,使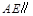 平面
平面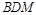 ?若存在,求
?若存在,求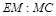 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.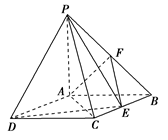
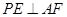 ;
;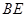 为何值时,
为何值时, 与平面
与平面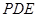 所成角的大小为45°.
所成角的大小为45°.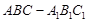 中,
中,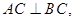
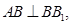
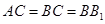 ,
,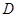 为
为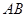 的中点,且
的中点,且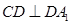 .
.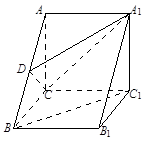
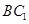 ∥平面
∥平面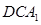 ;
;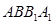 所成角的大小.
所成角的大小.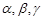 是两两不重合的三个平面,下列命题中错误的是( )
是两两不重合的三个平面,下列命题中错误的是( ) 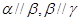 ,则
,则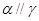
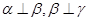 ,则
,则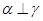
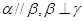 ,则
,则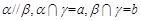 ,则
,则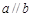
 中,
中, 、
、 分别为棱
分别为棱 、
、 的中点,则在空间中与直线
的中点,则在空间中与直线 、
、 、CD都相交的直线有
、CD都相交的直线有