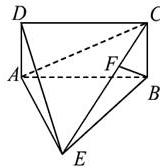
题目内容
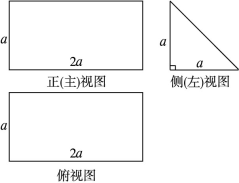
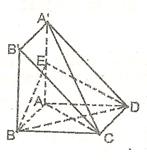
一个多面体的直观图和三视图如图所示,其中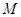 ,
,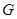 分别是
分别是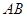 ,
,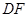 的中点.
的中点.
(1)求证: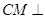 平面
平面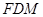 ;
;
(2)在线段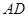 上(含
上(含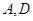 端点)确定一点
端点)确定一点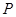 ,使得
,使得 ∥平面
∥平面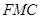 ,并给出证明.
,并给出证明.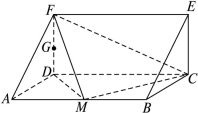
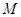 ,
,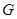 分别是
分别是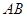 ,
,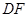 的中点.
的中点.(1)求证:
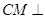 平面
平面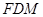 ;
;(2)在线段
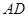 上(含
上(含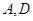 端点)确定一点
端点)确定一点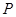 ,使得
,使得 ∥平面
∥平面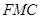 ,并给出证明.
,并给出证明.

(1)分别证明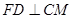 ,
,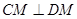 ,根据线面平行的判定定理即可证明
,根据线面平行的判定定理即可证明
(2)点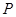 在
在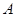 点处
点处
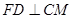 ,
,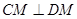 ,根据线面平行的判定定理即可证明
,根据线面平行的判定定理即可证明(2)点
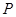 在
在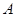 点处
点处试题分析:由三视图可得直观图为直三棱柱且底面
 中
中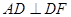 ,
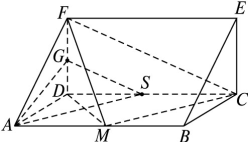
,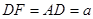 .
.
(1)∵
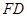 ⊥平面
⊥平面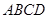 ,
, ?平面
?平面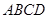 ,
,∴
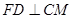 .
.在矩形
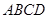 中,
中,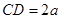 ,
,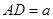 ,
,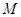 为
为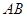 中点,
中点, ,
,∴
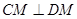 .
.∵
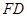 ?平面
?平面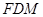 ,
, ?平面
?平面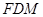 ,
,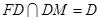 ,
,∴
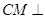 平面
平面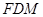 . …6分
. …6分(2)点
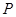 在
在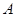 点处.
点处.证明:取
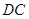 中点
中点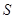 ,连接
,连接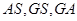 ,
,∵
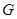 是
是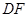 的中点,∴
的中点,∴ . 又
. 又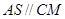 ,
, ,
,∴平面
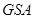 ∥平面
∥平面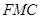 .而
.而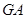 ?平面
?平面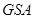 ,
,∴
 ∥平面
∥平面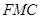 . …14分
. …14分点评:证明直线、平面间的位置关系,要紧扣相应的判定定理和性质定理,定理中要求的条件缺一不可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
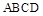 与
与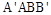 都是边长为
都是边长为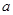 的正方形,点E是
的正方形,点E是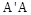 的中点,
的中点,
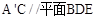 ;
;  ;
;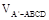 与
与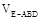 的比值。
的比值。 的底面是正方形,
的底面是正方形, ,点
,点 在棱
在棱 上.
上.
 平面
平面 ;
; ,且
,且 时,确定点
时,确定点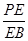 的值.
的值.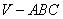 底面为正三角形,侧面
底面为正三角形,侧面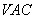 与底面垂直且
与底面垂直且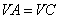 ,已知其主视图的面积为
,已知其主视图的面积为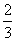 ,则其左视图的面积为
,则其左视图的面积为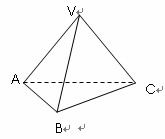
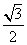

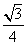
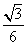
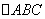 是边长为
是边长为 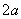 的等边三角形,
的等边三角形, 是分别以
是分别以 为底的全等的等腰三角形,现将该平面图形分别沿
为底的全等的等腰三角形,现将该平面图形分别沿 垂直,连接
垂直,连接 ,得到图二所示的几何体,据此几何体解决下面问题.
,得到图二所示的几何体,据此几何体解决下面问题.
 ;
; 时,求三棱锥
时,求三棱锥 的体积
的体积 ;
; 的余弦值.
的余弦值.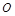 为正方形
为正方形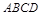 的中心,四边形
的中心,四边形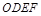 是平行四边形,且平面
是平行四边形,且平面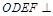 平面
平面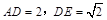 .
.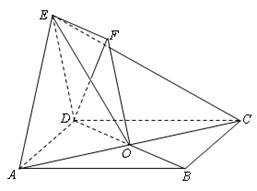
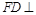 平面
平面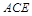 .
. 上是否存在一点
上是否存在一点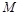 ,使
,使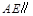 平面
平面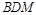 ?若存在,求
?若存在,求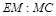 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.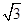 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.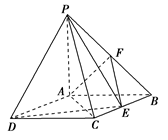
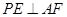 ;
;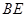 为何值时,
为何值时, 与平面
与平面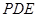 所成角的大小为45°.
所成角的大小为45°.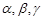 是两两不重合的三个平面,下列命题中错误的是( )
是两两不重合的三个平面,下列命题中错误的是( ) 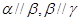 ,则
,则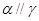
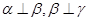 ,则
,则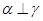
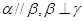 ,则
,则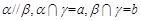 ,则
,则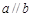
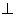 平面ABCD,AE=EB=BC=2,F为CE上的点,且BF
平面ABCD,AE=EB=BC=2,F为CE上的点,且BF