题目内容
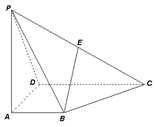
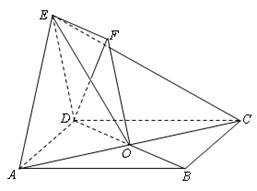
如图,四棱锥 的底面
的底面 为一直角梯形,其中
为一直角梯形,其中 ,
,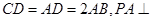 底面
底面 ,
, 是
是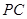 的中点.
的中点.
(Ⅰ)求证: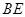 //平面
//平面 ;
;
(Ⅱ)若 平面
平面 ,求平面
,求平面 与平面
与平面 夹角的余弦值.
夹角的余弦值.
 的底面
的底面 为一直角梯形,其中
为一直角梯形,其中 ,
,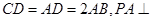 底面
底面 ,
, 是
是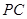 的中点.
的中点.
(Ⅰ)求证:
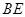 //平面
//平面 ;
;(Ⅱ)若
 平面
平面 ,求平面
,求平面 与平面
与平面 夹角的余弦值.
夹角的余弦值.(1)要证明线面平行,可以建立直角坐标系,然后借助于平面的法向量以直线的方向向量得垂直关系来证明。
(2)

试题分析:设
 ,建立空间坐标系,使得
,建立空间坐标系,使得 ,
, ,
, ,
, . 2分
. 2分(Ⅰ)
 ,
, ,
,所以
 ,
,  平面
平面 ,
, 平面
平面 . 5分
. 5分(Ⅱ)
 平面
平面 ,
, ,即
,即
 ,
, ,即
,即 .
.平面
 和平面
和平面 中,
中,
 ,
,所以平面
 的一个法向量为
的一个法向量为 ;平面
;平面 的一个法向量为
的一个法向量为 ;
; ,所以平面
,所以平面 与平面
与平面 夹角的余弦值为
夹角的余弦值为 . 12分
. 12分点评:主要是考查了运用空间向量来证明垂直以及二面角的平面角的 求解,属于基础题。

练习册系列答案
相关题目
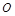 为正方形
为正方形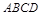 的中心,四边形
的中心,四边形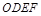 是平行四边形,且平面
是平行四边形,且平面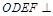 平面
平面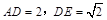 .
.
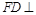 平面
平面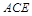 .
. 上是否存在一点
上是否存在一点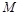 ,使
,使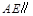 平面
平面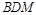 ?若存在,求
?若存在,求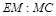 的值;若不存在,请说明理由.
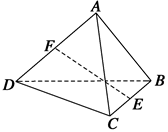
的值;若不存在,请说明理由. 中,
中, 、
、 分别为棱
分别为棱 、
、 的中点,则在空间中与直线
的中点,则在空间中与直线 、
、 、CD都相交的直线有
、CD都相交的直线有
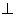 平面ABCD,AE=EB=BC=2,F为CE上的点,且BF
平面ABCD,AE=EB=BC=2,F为CE上的点,且BF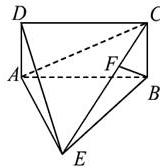
 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
 中,各棱长相等,侧棱垂直于底面,点
中,各棱长相等,侧棱垂直于底面,点 是侧面
是侧面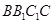 的中心,则
的中心,则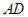 与平面
与平面
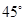
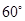
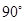
 BB1,C1F=
BB1,C1F=