题目内容
已知直线l1:x+a2y+1=0和直线l2:(a2+1)x-by+3=0(a,b∈R).
(1)若l1∥l2,求b的取值范围;
(2)若l1⊥l2,求|ab|的最小值.
(1)若l1∥l2,求b的取值范围;
(2)若l1⊥l2,求|ab|的最小值.
(1)(-∞,-6)∪(-6,0]
(2)2
(2)2
解:(1)因为l1∥l2,
所以-b-(a2+1)a2=0,
即b=-a2(a2+1)=-a4-a2
=-(a2+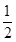 )2+
)2+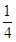 .
.
因为a2≥0,所以b≤0.
又因为a2+1≠3,所以b≠-6.
故b的取值范围是(-∞,-6)∪(-6,0].
(2)因为l1⊥l2,
所以(a2+1)-a2b=0.
显然a≠0,所以ab=a+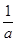 ,
,
|ab|=|a+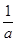 |≥2,
|≥2,
当且仅当a=±1时等号成立,
因此|ab|的最小值为2.
所以-b-(a2+1)a2=0,
即b=-a2(a2+1)=-a4-a2
=-(a2+
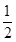 )2+
)2+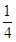 .
.因为a2≥0,所以b≤0.
又因为a2+1≠3,所以b≠-6.
故b的取值范围是(-∞,-6)∪(-6,0].
(2)因为l1⊥l2,
所以(a2+1)-a2b=0.
显然a≠0,所以ab=a+
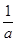 ,
,|ab|=|a+
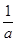 |≥2,
|≥2,当且仅当a=±1时等号成立,
因此|ab|的最小值为2.

练习册系列答案
相关题目
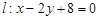 和两点
和两点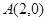 ,
,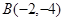 ,若直线
,若直线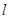 上存在点
上存在点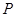 使得
使得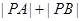 最小,则点
最小,则点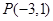 且与直线
且与直线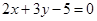 斜率相等的直线方程为 .
斜率相等的直线方程为 .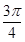 ,直线l1经过点A(3,2)和B(a,-1),且直线l1与直线l垂直,直线l2的方程为2x+by+1=0,且直线l2与直线l1平行,则a+b等于( )
,直线l1经过点A(3,2)和B(a,-1),且直线l1与直线l垂直,直线l2的方程为2x+by+1=0,且直线l2与直线l1平行,则a+b等于( )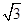 与直线2x+3y-6=0的交点位于第一象限,则直线l的倾斜角的取值范围是( )
与直线2x+3y-6=0的交点位于第一象限,则直线l的倾斜角的取值范围是( )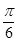 ,
,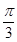 )
)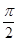 )
) ,则动点P的轨迹方程是( )
,则动点P的轨迹方程是( )



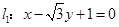 ,
,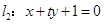 ,若直线
,若直线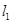 与
与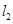 的夹角为
的夹角为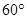 ,则
,则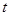 = .
= .