题目内容
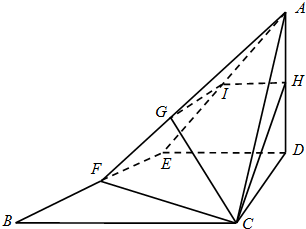
3.△ABC为等腰直角三角形,AC=BC=4,∠ACB=90°,D、E分别是边AC和AB的中点,现将△ADE沿DE折起,使面ADE⊥面DEBC,H是边AD的中点,平面BCH与AE交于点I.
(Ⅰ)求证:IH∥BC;
(Ⅱ)求三棱锥A-HIC的体积.
分析 (Ⅰ)证明ED∥平面BCH,ED∥HI,然后利用平行公理证明IH∥BC.、
(Ⅱ)求出棱锥的底面面积以及高,即可求解体积.
解答 (Ⅰ)证明:因为D、E分别是边AC和AB的中点,
所以ED∥BC,
因为BC?平面BCH,ED?平面BCH,
所以ED∥平面BCH
因为ED?平面BCH,ED?平面AED,平面BCH∩平面AED=HI
所以ED∥HI
又因为ED∥BC,
所以IH∥BC.…(6分)
(Ⅱ)解:VA-CIH=VC-AIH,
${S_{△AIC}}=\frac{1}{2}×1×1=\frac{1}{2}$
高CD=2,
$V=\frac{1}{3}×\frac{1}{2}×2=\frac{1}{3}$…(12分)
点评 本题考查几何体的体积的求法,转化思想的应用,直线与直线平面的证明,直线与平面平行的判定定理的应用.考查空间想象能力以及计算能力.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
18.在△ABC中,$AB=\sqrt{3}$,AC=1,∠B=30°,△ABC的面积为$\frac{{\sqrt{3}}}{2}$,则∠C=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
15.执行如图所示的程序框图,则输出s的值为( )


| A. | $\frac{3}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{5}{6}$ | D. | 5 |
12.设a>b>0,则a+$\frac{1}{b}$+$\frac{1}{a-b}$的最小值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 3+2$\sqrt{2}$ |