题目内容
11.△ABC为等腰直角三角形,AC=BC=4,∠ACB=90°,D、E分别是边AC和AB的中点,现将△ADE沿DE折起,使面ADE⊥面DEBC,H、F分别是边AD和BE的中点,平面BCH与AE、AF分别交于I、G两点.(Ⅰ)求证:IH∥BC;
(Ⅱ)求二面角A-GI-C的余弦值;
(Ⅲ)求AG的长.
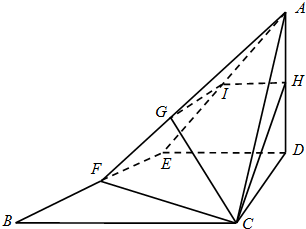
分析 (Ⅰ)证明ED∥BC,推出ED∥平面BCH,利用直线与平面平行的性质定理以及平行公理证明IH∥BC.
(Ⅱ)建立空间右手直角坐标系,求出平面AGI的一个法向量,平面CHI的一个法向量,利用向量的数量积求解二面角A-GI-C的余弦值.
(Ⅲ)法(一)$\overrightarrow{AG}=λ\overrightarrow{AF}=(3λ,λ,-2λ)$,通过$\overrightarrow{GH}•\overrightarrow{n_2}=0$,解得$λ=\frac{2}{3}$,然后求解即可.
法(二)取CD中点J,连接AJ交CH于点K,连接HJ,通过△HKJ与△CKA相似,求解即可.
解答 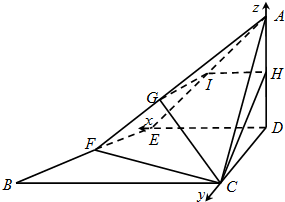 (Ⅰ)证明:因为D、E分别是边AC和AB的中点,
(Ⅰ)证明:因为D、E分别是边AC和AB的中点,
所以ED∥BC,
因为BC?平面BCH,ED?平面BCH,
所以ED∥平面BCH
因为ED?平面BCH,ED?平面AED,平面BCH∩平面AED=HI
所以ED∥HI
又因为ED∥BC,
所以IH∥BC.…(4分)
(Ⅱ)解:如图,建立空间右手直角坐标系,由题意得,D(0,0,0),E(2,0,0),A(0,0,2),F(3,1,0),C(0,2,0),H(0,0,1),$\overrightarrow{EA}=(-2,0,2)$,$\overrightarrow{EF}=(1,1,0)$,$\overrightarrow{CH}=(0,-2,1)$,$\overrightarrow{HI}=\frac{1}{2}\overrightarrow{DE}=(1,0,0)$,
设平面AGI的一个法向量为$\overrightarrow{n_1}=({x_1},{y_1},{z_1})$,则$\left\{\begin{array}{l}\overrightarrow{EA}•\overrightarrow{n_1}=0\\ \overrightarrow{EB}•\overrightarrow{n_1}=0\end{array}\right.$,$\left\{\begin{array}{l}-{x}_{1}+{z}_{1}=0\\{x}_{1}+{y}_{1}=0\end{array}\right.$,令z1=1,解得x1=1,y1=-1,则$\overrightarrow{n_1}=(1,-1,1)$
设平面CHI的一个法向量为$\overrightarrow{n_2}=({x_2},{y_2},{z_2})$,则$\left\{\begin{array}{l}\overrightarrow{CH}•\overrightarrow{n_2}=0\\ \overrightarrow{HI}•\overrightarrow{n_2}=0\end{array}\right.$,$\left\{\begin{array}{l}-2{y}_{1}+{z}_{2}=0\\{x}_{2}=0\end{array}\right.$,令z2=-2,解得y1=-1,则$\overrightarrow{n_2}=(0,-1,-2)$,$cos<\overrightarrow{n_1},\overrightarrow{n_2}>=\frac{{|{1-2}|}}{{\sqrt{3}•\sqrt{5}}}=\frac{{\sqrt{15}}}{15}$,
所以二面角A-GI-C的余弦值为$\frac{{\sqrt{15}}}{15}$…(8分)
(Ⅲ)解:法(一)$\overrightarrow{AF}=(3,1,-2)$,设$\overrightarrow{AG}=λ\overrightarrow{AF}=(3λ,λ,-2λ)$$\overrightarrow{GH}=\overrightarrow{AH}-\overrightarrow{AG}=(0,0,-1)-(3λ,λ,-2λ)=(-3λ,-λ,2λ-1)$
则$\overrightarrow{GH}•\overrightarrow{n_2}=0$,解得$λ=\frac{2}{3}$,$AG=\frac{2}{3}AF=\frac{2}{3}\sqrt{{3^2}+1+{{(-2)}^2}}=\frac{{2\sqrt{14}}}{3}$…(12分)
法(二)取CD中点J,连接AJ交CH于点K,连接HJ,△HKJ与△CKA相似,
得$\frac{AK}{KJ}=2$,易证HI∥GK,所以$AG=\frac{2}{3}AF=\frac{{2\sqrt{14}}}{3}$…(12分)
点评 本题考查空间向量求解二面角的平面角的大小,直线与平面平行的性质定理以及判定定理的应用,空间距离的求法,考查计算能力以及空间想象能力.

| 统计信息 | 在不堵车的情况下到达城市乙所需时间(天) | 在堵车的情况下到达城市乙所需时间(天) | 堵车的概率 | 运费(万元) |
| 公路1 | 2 | 3 | $\frac{1}{10}$ | 1.6 |
| 公路2 | 1 | 4 | $\frac{1}{2}$ | 0.8 |
(Ⅱ)如果你是牛奶厂的决策者,你选择哪条公路运送牛奶有可能让牛奶厂获得的毛收入更多?
(注:毛收入=销售商支付给牛奶厂的费用-运费)
| A. | 向右平移$\frac{π}{12}$个单位 | B. | 向左平移$\frac{π}{12}$个单位 | ||
| C. | 向右平移$\frac{π}{6}$个单位 | D. | 向左平移$\frac{π}{6}$个单位 |
| A. | $\frac{3}{5}$ | B. | $\frac{35}{9}$ | C. | $\frac{10}{3}$ | D. | -$\frac{1}{3}$ |
| A. | A与B相互独立 | B. | P(AB)=P(A)•P(B) | C. | A与$\overline{B}$不相互独立 | D. | P(AB)=$\frac{1}{4}$ |
