题目内容
15.执行如图所示的程序框图,则输出s的值为( )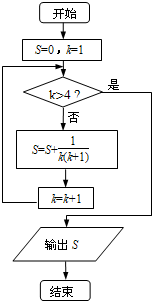
| A. | $\frac{3}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{5}{6}$ | D. | 5 |
分析 模拟执行程序框图,依次写出每次循环得到的S,k的值,当k=5时,满足条件k>4,退出循环,输出S的值为$\frac{4}{5}$.
解答 解:模拟执行程序框图,可得
S=0,k=1
不满足条件k>4,S=$\frac{1}{1×2}$,k=2
不满足条件k>4,S=$\frac{1}{1×2}$+$\frac{1}{2×3}$,k=3
不满足条件k>4,S=$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$,k=4
不满足条件k>4,S=$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+$\frac{1}{4×5}$,k=5
满足条件k>4,退出循环,输出S的值.
S=$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+$\frac{1}{4×5}$=$1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}$=$\frac{4}{5}$.
故选:B.
点评 本题主要考查了循环结构的程序框图,用裂项法求值是解题的关键,属于基本知识的考查.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
20.已知在平面直角坐标系中,点P是直线l:l=-$\frac{1}{2}$上一动点,定点F($\frac{1}{2}$,0),点Q为PF的中点,动点M满足$\overrightarrow{MQ}$•$\overrightarrow{PF}$=0,$\overrightarrow{MP}$=λ$\overrightarrow{OF}$(λ∈R).过点M作圆(x-3)2+y2=2的切线,切点分别为S,T,则$\overrightarrow{MS}$•$\overrightarrow{MT}$的最小值是( )
| A. | $\frac{3}{5}$ | B. | $\frac{35}{9}$ | C. | $\frac{10}{3}$ | D. | -$\frac{1}{3}$ |
5.已知|$\overrightarrow{a}$|=1,$\overrightarrow{b}$=(0,2),且$\overrightarrow{a}•\overrightarrow{b}$=$\sqrt{3}$,则向量$\overrightarrow{a}$与$\overrightarrow{b}$夹角的大小为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |