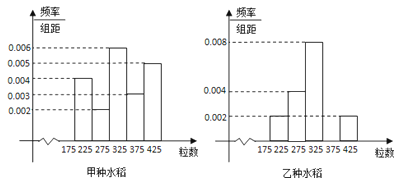
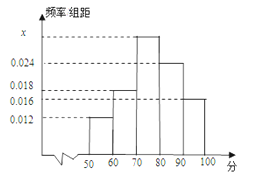
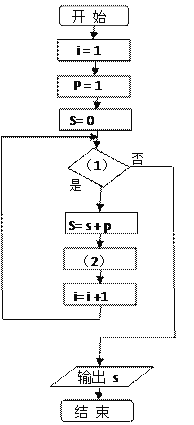
题目内容
【题目】三国时期赵爽在《勾股方圆图注》中对勾股定理的证明可用现代数学表述为如图所示，我们教材中利用该图作为“（ ）”的几何解释．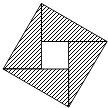 
A.如果a＞b，b＞c，那么a＞c
B.如果a＞b＞0，那么a2＞b2
C.对任意实数a和b，有a2+b2≥2ab，当且仅当a=b时等号成立
D.如果a＞b，c＞0那么ac＞bc
【答案】C
【解析】解：可将直角三角形的两直角边长度取作a，b，斜边为c（c2=a2+b2），
则外围的正方形的面积为c2 ， 也就是a2+b2 ， 四个阴影面积之和刚好为2ab，
对任意正实数a和b，有a2+b2≥2ab，当且仅当a=b时等号成立．
故选：C．
【考点精析】解答此题的关键在于理解基本不等式的相关知识，掌握基本不等式：
,（当且仅当
时取到等号）；变形公式：
．
练习册系列答案
相关题目
