��Ŀ����
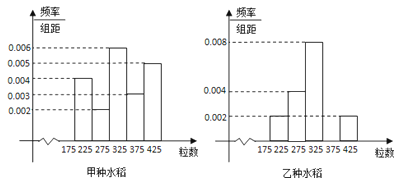
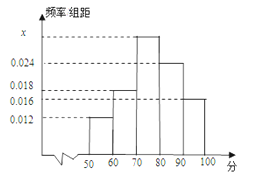
����Ŀ��ijѧУ�о���ѧϰС��Ը�У����ѧ������������е��飬�ڸ�����ȫ��![]() ��ѧ���������ȡ��
��ѧ���������ȡ��![]() ��ѧ�������������õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ��
��ѧ�������������õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ��
�꼶���� �Ƿ���� |
|
|
���� |
|
|
������ |
|
|
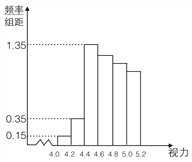
��1����ֱ��ͼ�к������Ƶ���ɵȲ����У��Թ���ȫ�꼶������![]() ���µ�������
���µ�������
��2��ѧϰС���Ա���֣�ѧϰ�ɼ�ͻ����ѧ�������ӵıȽ϶࣬Ϊ���о�ѧ����������ѧϰ�ɼ��Ƿ��й�ϵ�����꼶������![]() ����
����![]() ����ѧ�������˵��飬�õ��ұ������ݣ����ݱ��е����ݣ��ܷ��ڷ����ĸ��ʲ�����
����ѧ�������˵��飬�õ��ұ������ݣ����ݱ��е����ݣ��ܷ��ڷ����ĸ��ʲ�����![]() ��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ?
��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ?
��3���ڣ����е����![]() ��ѧ���У����շֲ�����ڲ����ӵ�ѧ���г�ȡ��
��ѧ���У����շֲ�����ڲ����ӵ�ѧ���г�ȡ��![]() �ˣ���һ�������������õĻ���ϰ�ߣ���������
�ˣ���һ�������������õĻ���ϰ�ߣ���������![]() ������ȡ
������ȡ![]() �ˣ���������
�ˣ���������![]() ��ѧ������Ϊ
��ѧ������Ϊ![]() ����
����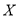 �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
|
|
|
|
|
|
|
|
|
|
| 7.879 |
![]()
���� 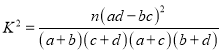
���𰸡�(1)820��(2) �ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ��(3)�𰸼�����.
��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ��(3)�𰸼�����.
�����������������(1)����ֱ��ͼ�е�ǰ�������ݺ͵Ȳ����еõ��������Ƶ�����ٹ�����Ƶ�ʺ�������(2)������![]() ��ʽ������⣬�������ٽ�ֵ�����������(3)д��������������п���ȡֵ�����ó����ηֲ��ĸ��ʹ�ʽ�����Ӧ�ĸ��ʣ����б��õ��ֲ��У����������ѧ���� .
��ʽ������⣬�������ٽ�ֵ�����������(3)д��������������п���ȡֵ�����ó����ηֲ��ĸ��ʹ�ʽ�����Ӧ�ĸ��ʣ����б��õ��ֲ��У����������ѧ���� .
�����������1����ֱ��ͼ��֪����һ����3�ˣ��ڶ�����7�ˣ���������27�ˣ�
����Ϊ�������Ƶ���ɵȲ����У����Ժ������Ƶ������Ϊ27,24,21,18����������
��![]() ���µ�Ƶ��Ϊ
���µ�Ƶ��Ϊ![]() ����ȫ�꼶������
����ȫ�꼶������![]() ���µ�����ԼΪ
���µ�����ԼΪ![]() ��
��
��2��![]() ��
��
����ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ��
��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ��
��3��������9�����꼶������![]() ����
����![]() ���ֱ���3�˺�6�ˣ�
���ֱ���3�˺�6�ˣ�
![]() ��ȡ0��1��2��3
��ȡ0��1��2��3
�� ![]() ��
�� ![]() ��
��
�� ![]() ��
�� ![]()
�� ![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() ����ѧ����
����ѧ����![]() .
.

 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�