题目内容
【题目】如图,正四棱锥![]() 中,
中, ![]() ,侧棱
,侧棱![]() 与底面
与底面![]() 所成角的正切值为
所成角的正切值为![]() .
.
(1)若![]() 是
是![]() 中点,求异面直线
中点,求异面直线![]() 与
与![]() 所成角的正切值;
所成角的正切值;
(2)求侧面![]() 与底面
与底面![]() 所成二面角的大小.
所成二面角的大小.
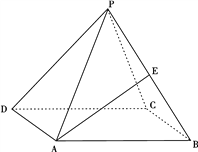
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)线线角找平行:取BD中点O,由三角形中位线性质得![]()
![]()
![]() ,即
,即![]() 就是异面直线PD与AE所成的角.再解三角形可得异面直线PD与AE所成角的正切值为
就是异面直线PD与AE所成的角.再解三角形可得异面直线PD与AE所成角的正切值为![]() ;(2)作OF⊥AD,因为PO⊥面ABCD,所以PF⊥AD,即得
;(2)作OF⊥AD,因为PO⊥面ABCD,所以PF⊥AD,即得![]() 就是侧面
就是侧面![]() 与底面
与底面![]() 所成二面角的平面角.再解三角形可得侧面
所成二面角的平面角.再解三角形可得侧面![]() 与底面
与底面![]() 所成二面角的大小为
所成二面角的大小为![]() .
.
试题解析:解:(1)连结EO,由于O为BD中点,E为PD中点,所以, ![]()
![]()
![]() .∴
.∴ ![]() 就是异面直线PD与AE所成的角.
就是异面直线PD与AE所成的角.
在Rt![]() 中,
中, ![]() .∴
.∴ ![]() .
.
由![]() ,
, ![]() 可知
可知![]() 面
面![]() .所以,
.所以, ![]()
在Rt![]() 中,
中, ![]() ,
,
即异面直线PD与AE所成角的正切值为![]() ;
;
(2) 连结![]() 交于点
交于点![]() ,连结PO,则PO⊥面ABCD,
,连结PO,则PO⊥面ABCD,
∴ ∠PAO就是![]() 与底面
与底面![]() 所成的角,
所成的角,
∴ tan∠PAO=![]() PO=AOtan∠PAO =
PO=AOtan∠PAO =![]() =
=![]() .
.
设F为AD中点,连FO、PF,
易知OF⊥AD,PF⊥AD,所以![]() 就是侧面
就是侧面![]() 与底面
与底面![]() 所成二面角的平面角.
所成二面角的平面角.
在Rt![]() 中,
中, ![]() ,
,
∴![]() ,即侧面
,即侧面![]() 与底面
与底面![]() 所成二面角的大小为
所成二面角的大小为![]() .
.

【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年龄45岁为分界点”,由以上统计数据完成下面![]() 列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若从年龄在[25,35)和[55,65)的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在[55,65)的概率.
参考数据如下:
附临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() 的观测值:
的观测值: ![]() (其中
(其中![]() )
)