题目内容
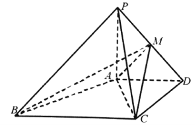
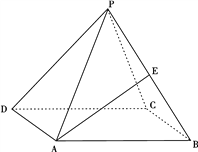
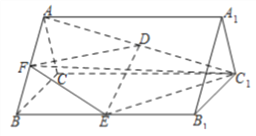
【题目】如图,在正三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 和
和![]() 的中点.
的中点.
(1)求证: ![]() //平面
//平面![]() ;
;
(2)若![]() 为
为![]() 中点,求三棱锥
中点,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)取![]() 中点
中点![]() ,利用平几知识可得
,利用平几知识可得![]() 是平行四边形,即得
是平行四边形,即得![]() ,再根据线面平行判定定理得
,再根据线面平行判定定理得![]() //平面
//平面![]() ;(2)利用等体积性质进行转化:
;(2)利用等体积性质进行转化: ![]()
![]()
![]() ,最后根据锥体体积公式求体积
,最后根据锥体体积公式求体积
试题解析:(Ⅰ)证明:取![]() 中点
中点![]() ,连接
,连接![]() 和
和![]() ,因为
,因为![]() 和
和![]() 分别为
分别为![]() 和
和![]() 的中点,所以
的中点,所以![]() ,且
,且![]() ,则
,则![]() 是平行四边形,
是平行四边形, ![]() ,又
,又![]()
![]() ,所以
,所以![]() //平面
//平面![]() ;
;
(Ⅱ)因为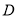 为
为![]() 的中点,所以
的中点,所以![]() , 又
, 又![]() 为
为![]() 中点,所以
中点,所以![]() ,则
,则![]()
![]()
![]()
![]() .
.
点睛:垂直、平行关系证明中应用转化与化归思想的常见类型.
(1)证明线面、面面平行,需转化为证明线线平行.
(2)证明线面垂直,需转化为证明线线垂直.
(3)证明线线垂直,需转化为证明线面垂直.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】为了研究某种微生物的生长规律,需要了解环境温度![]() (
(![]() )对该微生物的活性指标
)对该微生物的活性指标![]() 的影响,某实验小组设计了一组实验,并得到如表的实验数据:
的影响,某实验小组设计了一组实验,并得到如表的实验数据:
环境温度 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
活性指标 |
|
|
|
|
|
|
|
(Ⅰ)由表中数据判断![]() 关于
关于![]() 的关系较符合
的关系较符合![]() 还是
还是![]() ,并求
,并求![]() 关于
关于![]() 的回归方程(
的回归方程(![]() ,
,![]() 取整数);
取整数);
(Ⅱ)根据(Ⅰ)中的结果分析:若要求该种微生物的活性指标不能低于![]() ,则环境温度应不得高于多少
,则环境温度应不得高于多少![]() ?
?
附: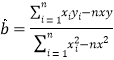 ,
,![]()
【题目】我国古代数学名著《续古摘奇算法》(杨辉)一书中有关于三阶幻方的问题:将1,2,3,4,5,6,7,8,9分别填入![]() 的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
8 | 3 | 4 |
1 | 5 | 9 |
6 | 7 | 2 |
A. 9 B. 8 C. 6 D. 4
【题目】重庆市乘坐出租车的收费办法如下:
⑴不超过3千米的里程收费10元; ⑵超过3千米的里程按每千米2元收费(对于其中不足千米的部分,若其小于0.5千米则不收费,若其大于或等于0.5千米则按1千米收费); 当车程超过3千米时,另收燃油附加费1元. |

相应系统收费的程序框图如图所示,其中![]() (单位:千米)为行驶里程,
(单位:千米)为行驶里程,![]() (单位:元)为所收费用,用
(单位:元)为所收费用,用![]() 表示不大于
表示不大于![]() 的最大整数,则图中①处应填( )
的最大整数,则图中①处应填( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()