题目内容
19.已知椭圆C的两个焦点分别为F1(-$\sqrt{10}$,0),F2($\sqrt{10}$,0),且椭圆C过点P(3,2).(Ⅰ)求椭圆C的标准方程;
(Ⅱ)与直线OP平行的直线交椭圆C于A,B两点,求△PAB面积的最大值.
分析 (Ⅰ)由题意设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,利用椭圆定义求得a,结合隐含条件求得b,则椭圆方程可求;
(Ⅱ)求出kOP=$\frac{2}{3}$,设与直线OP平行的直线方程为y=$\frac{2}{3}$x+m,联立直线和椭圆方程,运用韦达定理和判别式大于0,以及弦长公式,点到直线的距离公式和三角形的面积公式,结合基本不等式即可得到所求最大值.
解答 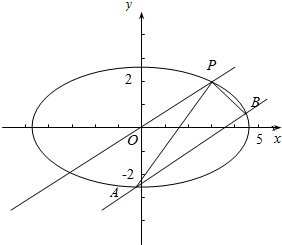 解:(Ⅰ)由题意设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,
解:(Ⅰ)由题意设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,
∵椭圆C的两个焦点分别为F1(-$\sqrt{10}$,0),
F2($\sqrt{10}$,0),且椭圆C过点P(3,2),
由椭圆定义可得2a=$\sqrt{(3+\sqrt{10})^{2}+{2}^{2}}$+$\sqrt{(3-\sqrt{10})^{2}+{2}^{2}}$=6$\sqrt{2}$,即a=3$\sqrt{2}$,
∴b2=a2-c2=8,
则椭圆C的标准方程为$\frac{{x}^{2}}{18}$+$\frac{{y}^{2}}{8}$=1;
(Ⅱ)由kOP=$\frac{2}{3}$,
设与直线OP平行的直线方程为y=$\frac{2}{3}$x+m,
联立$\left\{\begin{array}{l}{y=\frac{2}{3}x+m}\\{\frac{{x}^{2}}{18}+\frac{{y}^{2}}{8}=1}\end{array}\right.$,得8x2+12mx+9m2-72=0.
由判别式△=144m2-32(9m2-72)>0,解得0<|m|<4.
设A(x1,y1),B(x2,y2),则x1+x2=-$\frac{3}{2}$m,x1x2=$\frac{9{m}^{2}-72}{8}$,
|AB|=$\sqrt{1+\frac{4}{9}}$•$\sqrt{\frac{9}{4}{m}^{2}-\frac{9{m}^{2}-72}{2}}$=$\frac{\sqrt{13}}{3}$•$\frac{\sqrt{144-9{m}^{2}}}{2}$,
点O到直线AB的距离为d=$\frac{|m|}{\sqrt{1+\frac{4}{9}}}$=$\frac{3}{\sqrt{13}}$|m|,
即有△PAB面积为S=$\frac{1}{2}$|AB|d=$\frac{|m|\sqrt{144-9{m}^{2}}}{4}$=$\frac{\sqrt{9{m}^{2}(144-9{m}^{2})}}{12}$≤$\frac{\sqrt{(\frac{144}{2})^{2}}}{12}$=6.
当且仅当9m2=144-9m2,即m=±2$\sqrt{2}$时,取得最大值6.
点评 本题考查椭圆方程的求法,考查直线和椭圆方程联立,运用韦达定理和弦长公式,以及点到直线的距离公式,考查计算能力,是中档题.

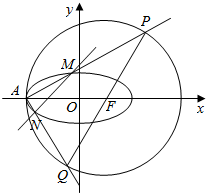 已知A(-2,0)是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)与圆F:(x-c)2+y2=9的一个交点,且圆心F是椭圆的一个焦点,
已知A(-2,0)是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)与圆F:(x-c)2+y2=9的一个交点,且圆心F是椭圆的一个焦点,