题目内容
9.$\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(-3,5),则$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为$\frac{9\sqrt{34}}{34}$.分析 由已知向量的坐标求出$\overrightarrow{a}•\overrightarrow{b}$与$|\overrightarrow{b}|$,代入投影公式得答案.
解答 解:∵$\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(-3,5),
∴$\overrightarrow{a}•\overrightarrow{b}=2×(-3)+3×5=9$,
$|\overrightarrow{b}|=\sqrt{(-3)^{2}+{5}^{2}}=\sqrt{34}$,
则$|\overrightarrow{a}|cos<\overrightarrow{a},\overrightarrow{b}>$=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}=\frac{9}{\sqrt{34}}=\frac{9\sqrt{34}}{34}$.
故答案为:$\frac{9\sqrt{34}}{34}$.
点评 本题考查平面向量的数量积运算,考查了向量在向量方向上的投影的概念,是基础题.

练习册系列答案
相关题目
20.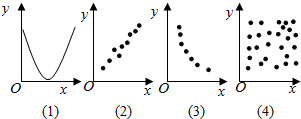 如图,两个变量具有相关关系的图是( )
如图,两个变量具有相关关系的图是( )
 如图,两个变量具有相关关系的图是( )
如图,两个变量具有相关关系的图是( )| A. | (1)(2) | B. | (1)(3) | C. | (2)(4) | D. | (2)(3) |
4.点$(\sqrt{2},\sqrt{3})$在双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)上,且C的焦距为4,则它的离心率为( )
| A. | 2 | B. | 4 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
 如图直角梯形OADC中,OA∥CD,∠D=60°,OA=1,CD=2,在梯形内挖去一个以OA为半径的四分之一圆,图中阴影部分绕OC所在直线旋转一周,求该旋转体的体积和表面积.
如图直角梯形OADC中,OA∥CD,∠D=60°,OA=1,CD=2,在梯形内挖去一个以OA为半径的四分之一圆,图中阴影部分绕OC所在直线旋转一周,求该旋转体的体积和表面积.