题目内容
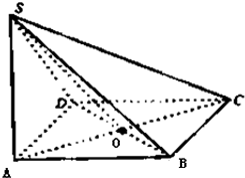
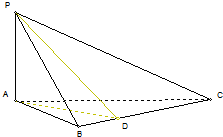
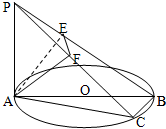
如图,AB为圆O的直径,点C为圆O上异于A、B的一点,PA⊥平面ABC,点A在PB、PC上的射影分别为点E、F.
(1)求证:PB⊥平面AFE;
(2)若AB=4,PA=3,BC=2,求三棱锥C-PAB的体积与此三棱锥的外接球(即点P、A、B、C都在此球面上)的体积之比.
(1)求证:PB⊥平面AFE;
(2)若AB=4,PA=3,BC=2,求三棱锥C-PAB的体积与此三棱锥的外接球(即点P、A、B、C都在此球面上)的体积之比.

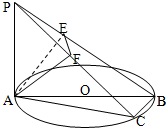
证明:(1)∵PA⊥面ABC,BC?面ABC,
∴BC⊥PA,又AB是圆O的直径,∴BC⊥AC
所以BC⊥面PAC,又因AF?面PAC,
所以AF⊥BC,又因AF⊥PC,
所以AF⊥面PBC,又因PB?面PBC,
所以PB⊥AF,又因PB⊥AE,所以PB⊥面AFE.(5分)
(2)VC-PAB=VP-ABC=
S△ABC•PA=
×
×AC•BC•PA=2
,
取PB的中点M,由直角三角形性质得,PM=AM=BM=CM,故三棱锥的外接球球心为M,
其半径为
PB=
,所以V球M=
π(
)3=
,体积之比为
.(10分)
∴BC⊥PA,又AB是圆O的直径,∴BC⊥AC
所以BC⊥面PAC,又因AF?面PAC,
所以AF⊥BC,又因AF⊥PC,
所以AF⊥面PBC,又因PB?面PBC,
所以PB⊥AF,又因PB⊥AE,所以PB⊥面AFE.(5分)
(2)VC-PAB=VP-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
取PB的中点M,由直角三角形性质得,PM=AM=BM=CM,故三棱锥的外接球球心为M,
其半径为
| 1 |
| 2 |
| 5 |
| 2 |
| 4 |
| 3 |
| 5 |
| 2 |
| 5π |
| 6 |
12
| ||
| 5π |


练习册系列答案
相关题目