题目内容
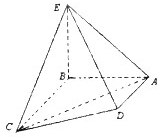
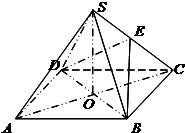
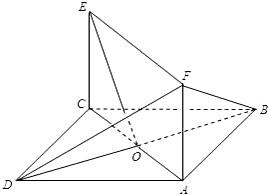
如图所示,正方形ABCD和矩形ACEF所在的平面相互垂直,已知AB=2,AF=
.
(I)求证:EO⊥平面BDF;
(II)求二面角A-DF-B的大小.
| 2 |
(I)求证:EO⊥平面BDF;
(II)求二面角A-DF-B的大小.

证明:(I)如图,正方形ABCD和矩形ACEF所在的平面相互垂直,对角线BD⊥AC,故有BD⊥平面ACEF,又EO?平面ACEF,故得BD⊥EO
又AB=2,AF=
.可求得AC=2
,即CO=AO=AF=CE=
,由于三角形ECO与三角形FAO都是直角三角形,故可得∠EOC=∠FOA=45°,所以∠EOF=90°,即EO⊥OF
又FO∩BD=O,故有EO⊥平面BDF
(II)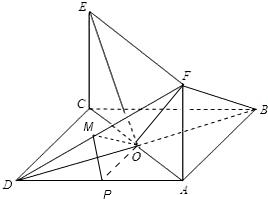 过O作OP⊥AD于P,过P作PM⊥DF于M,连接OM,
过O作OP⊥AD于P,过P作PM⊥DF于M,连接OM,
由题设条件知F-AD-O是直二面角,故可得OP⊥面ADF,由此可得OP⊥DF,由作图,PM⊥DF,故有DF⊥面OMP,所以OM⊥DF,由此可证得∠OMP即二面角的平面角,
在直线三角形DOA中,由于OA=OD,故P是AD中点,易得OP=1
在直角三角形DAF中可求得DF=
,由P是中点得DP=1,
由于△DAF≈△DMP,故有
=
得MP=
=
=
在直角三角形OPM中,tan∠OMP=
=
=
二面角A-DF-B的大小为60°
又AB=2,AF=
| 2 |
| 2 |
| 2 |
又FO∩BD=O,故有EO⊥平面BDF
(II)
 过O作OP⊥AD于P,过P作PM⊥DF于M,连接OM,
过O作OP⊥AD于P,过P作PM⊥DF于M,连接OM,由题设条件知F-AD-O是直二面角,故可得OP⊥面ADF,由此可得OP⊥DF,由作图,PM⊥DF,故有DF⊥面OMP,所以OM⊥DF,由此可证得∠OMP即二面角的平面角,
在直线三角形DOA中,由于OA=OD,故P是AD中点,易得OP=1
在直角三角形DAF中可求得DF=
| 6 |
由于△DAF≈△DMP,故有
| DP |
| DF |
| MP |
| AF |
| DP×AF |
| DF |
1×
| ||
|
| ||
| 3 |
在直角三角形OPM中,tan∠OMP=
| OP |
| MP |
| 1 | ||||
|
| 3 |
二面角A-DF-B的大小为60°

练习册系列答案
相关题目