题目内容
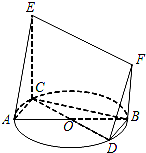
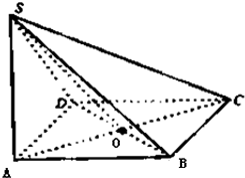
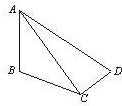
如图,AB,CD均为圆O的直径,CE⊥圆O所在的平面,BF∥CE.求证:
(1)平面BCEF⊥平面ACE;
(2)直线DF∥平面ACE.
(1)平面BCEF⊥平面ACE;
(2)直线DF∥平面ACE.

证明:(1)因为CE⊥圆O所在的平面,BC?圆O所在的平面,
所以CE⊥BC,…(2分)
因为AB为圆O的直径,点C在圆O上,所以AC⊥BC,…(3分)
因为AC∩CE=C,AC,CE?平面ACE,
所以BC⊥平面ACE,…(5分)
因为BC?平面BCEF,所以平面BCEF⊥平面ACE.…(7分)
(2)由(1)AC⊥BC,又因为CD为圆O的直径,
所以BD⊥BC,
因为AC,BC,BD在同一平面内,所以AC∥BD,…(9分)
因为BD?平面ACE,AC?平面ACE,所以BD∥平面ACE.…(11分)
因为BF∥CE,同理可证BF∥平面ACE,
因为BD∩BF=B,BD,BF?平面BDF,
所以平面BDF∥平面ACE,
因为DF?平面BDF,所以DF∥平面ACE.…(14分)
所以CE⊥BC,…(2分)
因为AB为圆O的直径,点C在圆O上,所以AC⊥BC,…(3分)
因为AC∩CE=C,AC,CE?平面ACE,
所以BC⊥平面ACE,…(5分)
因为BC?平面BCEF,所以平面BCEF⊥平面ACE.…(7分)
(2)由(1)AC⊥BC,又因为CD为圆O的直径,
所以BD⊥BC,
因为AC,BC,BD在同一平面内,所以AC∥BD,…(9分)
因为BD?平面ACE,AC?平面ACE,所以BD∥平面ACE.…(11分)
因为BF∥CE,同理可证BF∥平面ACE,
因为BD∩BF=B,BD,BF?平面BDF,
所以平面BDF∥平面ACE,
因为DF?平面BDF,所以DF∥平面ACE.…(14分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

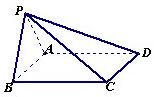
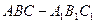 中,若
中,若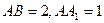 ,则点A到平面
,则点A到平面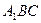 的距离为( )
的距离为( )