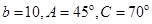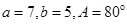题目内容
△ABC的内角A,B,C所对的边分别为a,b,c,且acosC+
c=b.
(1)求角A的大小;
(2)若△ABC的周长为3,求△ABC的面积的最大值.
| 1 |
| 2 |
(1)求角A的大小;
(2)若△ABC的周长为3,求△ABC的面积的最大值.
∵acosC+
c=b,
∴sinAcosC+
sinC=sinB=sin(A+C)=sinAcosC+cosAsinC,
整理得:
sinC=cosAsinC,
∵sinC≠0,
∴cosA=
,
∵A为三角形内角,
∴A=60°;
(2)∵A=60°,
∴a2=b2+c2-2bccosA=b2+c2-bc≥2bc-bc=bc,
∴a≥
,
∴3=a+b+c≥
+b+c≥
+2
=3
,即bc≤1,
∴S=
bcsinA=
bc≤
,当且仅当b=c=a=1时,取得最大值
.
| 1 |
| 2 |
∴sinAcosC+
| 1 |
| 2 |
整理得:
| 1 |
| 2 |
∵sinC≠0,
∴cosA=
| 1 |
| 2 |
∵A为三角形内角,
∴A=60°;
(2)∵A=60°,
∴a2=b2+c2-2bccosA=b2+c2-bc≥2bc-bc=bc,
∴a≥
| bc |
∴3=a+b+c≥
| bc |
| bc |
| bc |
| bc |
∴S=
| 1 |
| 2 |
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |

练习册系列答案
相关题目
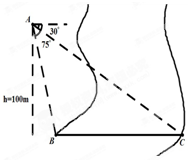
 ,
, 间的距离,海底探测仪沿水平方向在
间的距离,海底探测仪沿水平方向在 ,
, 两点进行测量,
两点进行测量,



 海里.
海里. 的面积;
的面积;
 中,满足下列条件的三角形有两个的是( ).
中,满足下列条件的三角形有两个的是( ).