题目内容
(1)设函数f(x)=(sinωx+cosωx)2+2cos2ωx(ω>0)的最小正周期为
,将y=f(x)的图象向右平移
个单位长度得到函数y=g(x)的图象,求y=g(x)的单调增区间.
(2)设△ABC的内角A、B、C的对边长分别为a、b、c,cos(A-C)+cosB=
,b2=ac,求角B的大小.
| 2π |
| 3 |
| π |
| 2 |
(2)设△ABC的内角A、B、C的对边长分别为a、b、c,cos(A-C)+cosB=
| 3 |
| 2 |
(1)f(x)=(sinωx+cosωx)2+2cos2ωx=sin2ωx+cos2ωx+sin2ωx+1+2cos2ωx
=sin2ωx+cos2ωx+2=
sin(2ωx+
)+2
依题意得
=
,
故ω=
,g(x)=
sin[3(x-
)+
]+2=
sin(3x-
)+2
由2kπ-
≤3x-
≤2kπ+
(k∈Z)
解得
kπ+
≤x≤
kπ+
(k∈Z)
故y=g(x)的单调增区间为:[
kπ+
,
kπ+
](k∈Z).
(2)由cos(A-C)+cosB=
及B=π-(A+C)得
cos(A-C)-cos(A+C)=
,
∴cosAcosC+sinAsinC-(cosAcosC-sinAsinC)=
,
∴sinAsinC=
.
又由b2=ac及正弦定理得sin2B=sinAsinC,
故sin2B=
,
∴sinB=
或sinB=-
(舍去),
于是B=
或B=
.
又由b2=ac
知b≤a或b≤c
∴B=
.
=sin2ωx+cos2ωx+2=
| 2 |
| π |
| 4 |
依题意得
| 2π |
| 2ω |
| 2π |
| 3 |
故ω=
| 3 |
| 2 |
| 2 |
| π |
| 2 |
| π |
| 4 |
| 2 |
| 5π |
| 4 |
由2kπ-
| π |
| 2 |
| 5π |
| 4 |
| π |
| 2 |
解得
| 2 |
| 3 |
| π |
| 4 |
| 2 |
| 3 |
| 7π |
| 12 |
故y=g(x)的单调增区间为:[
| 2 |
| 3 |
| π |
| 4 |
| 2 |
| 3 |
| 7π |
| 12 |
(2)由cos(A-C)+cosB=
| 3 |
| 2 |
cos(A-C)-cos(A+C)=
| 3 |
| 2 |
∴cosAcosC+sinAsinC-(cosAcosC-sinAsinC)=
| 3 |
| 2 |
∴sinAsinC=
| 3 |
| 4 |
又由b2=ac及正弦定理得sin2B=sinAsinC,
故sin2B=
| 3 |
| 4 |
∴sinB=
| ||
| 2 |
| ||
| 2 |
于是B=
| π |
| 3 |
| 2π |
| 3 |
又由b2=ac
知b≤a或b≤c
∴B=
| π |
| 3 |

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目

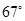 ,
,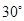 ,此时气球的高是
,此时气球的高是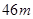 ,则河流的宽度BC约等于
,则河流的宽度BC约等于 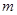 .(用四舍五入法将结果精确到个位.参考数据:
.(用四舍五入法将结果精确到个位.参考数据: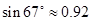 ,
,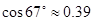 ,
,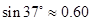 ,
,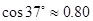 ,
,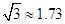 )
)