题目内容
在△ABC中,若A=60°,a=2
,则
等于( )
| 3 |
| a+b+c |
| sinA+sinB+sinC |
| A.1 | B.2
| C.4 | D.4
|
△ABC中,若A=60°,a=2
,则由正弦定理可得
=2R(R为△ABC的外接圆半径),
∴2R=
=4,∴
=
=2R=4,
故选:C.
| 3 |
| a |
| sinA |
∴2R=
2
| ||
| sin60° |
| a+b+c |
| sinA+sinB+sinC |
| 2RsinA+2RsinB+2RsinC |
| sinA+sinB+sinC |
故选:C.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 的图像过点
的图像过点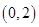 ,且函数
,且函数 图像的两相邻对称轴间的距离为
图像的两相邻对称轴间的距离为 .
. 时,求函数
时,求函数 的值域;
的值域; ,求函数
,求函数 的单调区间.
的单调区间. 两地相距
两地相距 ,且
,且 地在
地在 地的正东方。一人在
地的正东方。一人在 在正北方,建筑
在正北方,建筑 在北偏西
在北偏西 ;在
;在 ,建筑
,建筑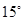 ,则两建筑
,则两建筑



 ,若
,若 ,则
,则 ( )
( )
