题目内容

△ABC的角A，B，C的对边分别为a，b，c，已知asinA+bsinB-csinC=asinB．
（Ⅰ）求角C；
（Ⅱ）若a+b=5，S△ABC=
3
2
3
，求c的值．
（Ⅰ）根据正弦定理
a
sinA
=
b
sinB
=
c
sinC
，
原等式可转化为：a2+b2-c2=ab，
∴cosC=
a2+b2-c2
2ab
=
1
2
，
∵C为三角形内角，
∴C=60°；
（Ⅱ）∵S△ABC=
1
2
absinC=
1
2
ab•
3
2
=
3
3
2
，
∴ab=6，
∵a+b=5，cosC=
1
2
，
∴由余弦定理得：c2=a2+b2-2ab•cosC=（a+b）2-3ab=25-18=7，
解得：c=
7
．
练习册系列答案
相关题目
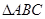在中，角所对的边分别为，且是方程的两个根，且，求：
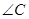（1）的度数；  （2）边的长度．
△ABC的三个内角A、B、C所对的边分别为a、b、c，c=3，C=60°，A=75°，则b的值=______．
设△ABC的内角A、B、C所对边分别是a、b、c，已知B=60°，
（1）若b=
3
，A=45°，求a；
（2）若a、b、c成等比数列，请判断△ABC的形状．
在△ABC中，角A，B，C所对的边分别为a，b，c，a=
2
，A=
π
4
，B=
π
3
，则△ABC的面积为S=______．
在△ABC中，a，b，c分别是BC，AC，AB三边的长，已知a=8，B=60°，C=75°，则b等于______．
己知△ABC的内角A、B、C的对边长分别为a、b、c．且asinA+csinC-
2
asinC=bsinB，
（1）求角B；
（2）若A=75°，b=2，求a．
△ABC的内角A，B，C所对的边分别为a，b，c，且acosC+
1
2
c=b．
（1）求角A的大小；
（2）若△ABC的周长为3，求△ABC的面积的最大值．
在△ABC中，内角A、B、C所对的边分别是a、b、c，若sinC＋sin(B－A)＝sin2A，则△ABC的形状为________．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网