题目内容
【题目】设函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 有两个极值点
有两个极值点![]() ,
,![]() ,求证:
,求证:![]() .
.
【答案】(1)当![]() 时,
时,![]() 在
在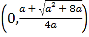 上单调递减,在
上单调递减,在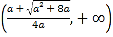 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 在
在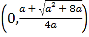 ,
,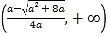 上单调递减,在
上单调递减,在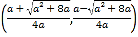 上单调递增.
上单调递增.
(2)见解析
【解析】
(1)求出![]() ,令
,令![]() ,
,![]() ,讨论
,讨论![]() 的取值,判断
的取值,判断![]() 的符号,从而可求出
的符号,从而可求出![]() 的单调性.
的单调性.
(2)由(1)得![]() 时,
时,![]() 有两个极值点
有两个极值点![]() ,设
,设![]() ,则有
,则有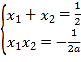 且
且![]() ,整理
,整理![]() ,
,![]() ,令
,令![]() ,
,![]() ,利用导数研究函数
,利用导数研究函数![]() 的单调性,可得
的单调性,可得![]() ,进而可得证
,进而可得证
解:(1)![]() ,
,
令![]() ,
,![]() ,
,
①当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
②当![]() 时,
时,![]() ,由
,由![]() 得
得![]() ,
,![]() ,
,
当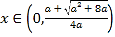 时
时![]() ,当
,当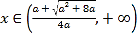 时,
时,![]() ,
,
∴![]() 在
在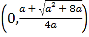 上单调递减,在
上单调递减,在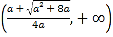 上单调递增,
上单调递增,
③当![]() 时,
时,![]() ,
,![]() ,∴
,∴![]() 在
在![]() 上单调递减,
上单调递减,
④当![]() 时,
时,![]() ,由
,由![]() 得
得![]() ,
,
当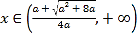 或
或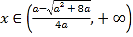 时,
时,![]() ,
,
当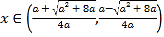 时,
时,![]() ,
,
∴![]() 在
在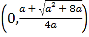 ,
,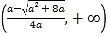 上单调递减,
上单调递减,
在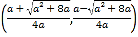 上单调递增,
上单调递增,
综上所述,
当![]() 时,
时,![]() 在
在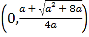 上单调递减,
上单调递减,
在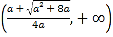 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 在
在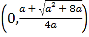 ,
,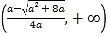 上单调递减,
上单调递减,
在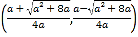 上单调递增.
上单调递增.
(2)由(1)得![]() 时,
时,![]() 有两个极值点
有两个极值点![]() ,设
,设![]() ,
,
则有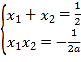 且
且![]() ,
,
∴![]()
![]()
![]()
![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
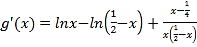 ,
,
令![]() ,则
,则
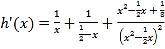 ,
,
∵![]() ,∴
,∴![]() ,
,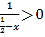 ,
,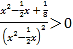 ,
,
∴当![]() 时,
时,![]() ,∴
,∴![]() 在区间
在区间![]() 单调递增,
单调递增,
∴![]() ,∴
,∴![]() 在区间
在区间![]() 单调递减,
单调递减,
∴![]() ,
,
综上,![]() .
.

 阅读快车系列答案
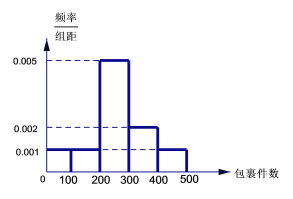
阅读快车系列答案【题目】某电视台举行文艺比赛,并通过网络对比赛进行直播.比赛现场有5名专家评委给每位参赛选手评分,场外观众可以通过网络给每位参赛选手评分.每位选手的最终得分由专家评分和观众评分确定.某选手参与比赛后,现场专家评分情况如表;场外有数万名观众参与评分,将评分按照[7,8),[8,9),[9,10]分组,绘成频率分布直方图如图:
专家 | A | B | C | D | E |
评分 | 9.6 | 9.5 | 9.6 | 8.9 | 9.7 |
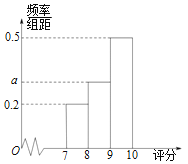
(1)求a的值,并用频率估计概率,估计某场外观众评分不小于9的概率;
(2)从5名专家中随机选取3人,X表示评分不小于9分的人数;从场外观众中随机选取3人,用频率估计概率,Y表示评分不小于9分的人数;试求E(X)与E(Y)的值;
(3)考虑以下两种方案来确定该选手的最终得分:方案一:用所有专家与观众的评分的平均数![]() 作为该选手的最终得分,方案二:分别计算专家评分的平均数
作为该选手的最终得分,方案二:分别计算专家评分的平均数![]() 和观众评分的平均数
和观众评分的平均数![]() ,用
,用![]() 作为该选手最终得分.请直接写出
作为该选手最终得分.请直接写出![]() 与
与![]() 的大小关系.
的大小关系.