Question

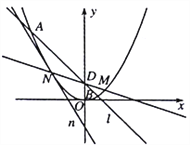
【题目】如图，在平面直角坐标系中，点在抛物线： 上，直线： 与抛物线交于， 两点，且直线， 的斜率之和为-1.

（1）求和的值；

（2）若，设直线与轴交于点，延长与抛物线交于点，抛物线在点处的切线为，记直线， 与轴围成的三角形面积为，求的最小值.

Answer 1

【答案】（1）， ；（2）.

【解析】试题分析：（1）将点代入抛物线： ，得，联立直线与抛物线方程，消去，得，则， ，由，求出；（2）求出直线DM的方程为，联立直线DM的方程和抛物线的方程，求出，利用导数的几何意义，求出切线n的斜率为，得到切线n的方程，联立直线DM、n的方程，求出Q点的纵坐标，且，采用导数的方法得出单调性，由单调性求出最小值。

试题解析：（1）将点代入抛物线： ，得，

，得，

设， ，则， ，

解法一： ，

由已知得，所以， .

解法二： ，

由已知得.

（2）在直线的方程中，令得， ，

直线的方程为： ，即，

由，得，

解得： ，或，所以，

由，得， ，切线的斜率，

切线的方程为： ，即，

由，得直线、交点，纵坐标，

在直线， 中分别令，得到与轴的交点， ，

所以 ， ， ，

当时，函数单调递减；当时，函数单调递增；

∴当时， 最小值为.