题目内容
11.某校高一年段为了控制学生迟到现象,特别规定在每周周一到周五这五天中,“连续5天,每天迟到都不超过5人次的班级才有资格争夺年段流动红旗”.根据过去5天年段统计的一到四班迟到学生人此数据的数字特征,一定有资格的是( )| A. | 一班:总体均值为2,总体方差为2 | B. | 二班:总体均值为3,中位数为3 | ||
| C. | 三班:总体均值为2,总体方差大于0 | D. | 四班:中位数为2,众数为2 |
分析 根据均值,中位数、众数、方差的意义,结合特殊数值逐一判断.
解答 解:A.总体均值为2,总体方差为2,当总体平均数是2,若有一个数据n超过5,则方差就会大于$\frac{1}{5}$[(n-2)2]≥$\frac{16}{5}$>2,由此每天迟到都不超过5人次,
B.总体均值为3,说明数据集中于3,中位数为3说明迟到3人的天数较多,但不能说明每天迟到都不超过5人,比如1,3,3,3,5
C.总体均值为2,说明数据集中于2,总体方差大于0,仍有可能某天迟到学生超过5人次
D 中位数为2,众数为2,比如0,1,2,2,6,6>5,不合要求.
故选:A.
点评 本题考查数据的几个特征量,这几个量各自表示数据的一个方面,有时候一个或两个量不能说明这组数据的特点,若要掌握这组数据则要全面掌握.

练习册系列答案
相关题目
19.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x≤1}\\{lo{g}_{3}(x-1),x>1}\end{array}\right.$,且f(x0)=1,则x0=( )
| A. | 0 | B. | 4 | C. | 0或4 | D. | 1或3 |
6.李明中午放学回家自己煮面条吃,有下面几道工序:①煮面条4分钟;②洗菜5分钟;③准备面条及佐料2分钟;④用锅把水烧开10分钟;⑤洗锅盛水2分钟.以上各道工序,除了④之外,一次只能进行一道工序,李明要将面条煮好,最少要用的分钟数为( )
| A. | 14 | B. | 15 | C. | 16 | D. | 23 |
3.已知全集U=Z,集合A={1,2},A∪B={1,2,3,4},那么(∁UA)∩B=( )
| A. | ∅ | B. | {x∈Z|x≥3} | C. | {3,4} | D. | {1,2} |
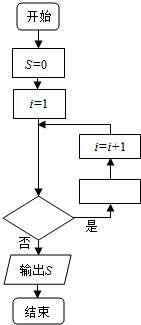 如图是计算1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2015}$的值的程序框图.
如图是计算1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2015}$的值的程序框图.


