题目内容
6.已知函数f(x)=2x与g(x)=x3的图象交于A(x1,y1)、B(x2,y2)两点,其中x1<x2.若x2∈(a,a+1),且a为整数,则a=( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
分析 构造函数h(x)=f(x)-g(x)=2x-x3,根据函数零点存在定理即可求出9<x2<10,再有x2∈(a,a+1),求出a的值.
解答 解:设h(x)=f(x)-g(x)=2x-x3,
当x=7时,h(7)=27-73=128-343<0,
当x=8时,h(8)=28-83=256-512<0,
当x=9时,h(9)=29-93=512-720<0,
当x=10时,h(10)=210-103=1024-1000>0,
∴9<x2<10,
∵x2∈(a,a+1),
∴a=9,
故选:C.
点评 本题考查函数零点存在定理,以及指数函数的和幂函数的图象与性质.

练习册系列答案
相关题目
17.已知α是第二象限角,sinα=$\frac{5}{13}$,则cosα=( )
| A. | -$\frac{5}{13}$ | B. | -$\frac{12}{13}$ | C. | $\frac{5}{13}$ | D. | $\frac{12}{13}$ |
14.已知函数y=2x2-2x+1的导数为y′,y′=( )
| A. | 2x-2 | B. | 4x+1 | C. | 4x-2 | D. | 2x+1 |
18.将正方形的每条边8等分,再取分点为顶点(不包括正方形的顶点),可以得到不同的三角形个数为( )
| A. | 1372 | B. | 2024 | C. | 3136 | D. | 4495 |
13.下列式子中,错误的是( )
| A. | $(\frac{1}{x})'=-\frac{1}{x^2}$ | B. | (cos(2x+1))′=-2sin(2x+1) | ||
| C. | $(x{log_a}x)'={log_a}x+\frac{1}{lna}$ | D. | $(\frac{{e}^{x}}{x})′=\frac{{e}^{x}•x+{e}^{x}}{{x}^{2}}$ |
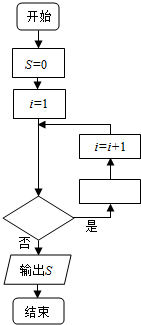 如图是计算1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2015}$的值的程序框图.
如图是计算1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2015}$的值的程序框图.



 已知函数$y=sin(ωx+φ)(ω>0,0<φ≤\frac{π}{2})$的部分图象如图所示.
已知函数$y=sin(ωx+φ)(ω>0,0<φ≤\frac{π}{2})$的部分图象如图所示.