题目内容
8.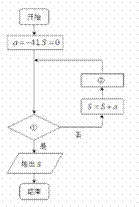 右图表示的是求首项为-41,公差为2的等差数列{an}前n项和的最小值的程序框图.①处可填写a>0;②处可填写a=a+2.
右图表示的是求首项为-41,公差为2的等差数列{an}前n项和的最小值的程序框图.①处可填写a>0;②处可填写a=a+2.
分析 由程序设计意图可知,②处应求通项,有a=a+2,又由此数列首项为负数,公差为正数,求前n项和的最小值只需累加至最后一个非正项即可,从而可求①处可填写:a>0.
解答 解:由程序设计意图可知,S表示此等差数列{an}前n项和,故②处应该填写a=a+2,
又因为此数列首项为负数,公差为正数,求前n项和的最小值只需累加至最后一个非正项即可,故①处可填写:a>0.
故答案为:a>0,a=a+2.
点评 本题主要考查了循环结构的程序框图,考查了等差数列的求和公式,算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.程序填空也是重要的考试题型,属于基础题.

练习册系列答案
相关题目
18.函数y=x-sinx,x∈[$\frac{π}{2}$,π]的最大值是( )
| A. | $\frac{π}{2}-1$ | B. | π-1 | C. | π | D. | π+1 |
19.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x≤1}\\{lo{g}_{3}(x-1),x>1}\end{array}\right.$,且f(x0)=1,则x0=( )
| A. | 0 | B. | 4 | C. | 0或4 | D. | 1或3 |
3.已知全集U=Z,集合A={1,2},A∪B={1,2,3,4},那么(∁UA)∩B=( )
| A. | ∅ | B. | {x∈Z|x≥3} | C. | {3,4} | D. | {1,2} |
13.圆C:x2+y2+4x-2y+3=0的圆心坐标及半径分别是( )
| A. | (-2,1),$\sqrt{2}$ | B. | (2,1),$\sqrt{2}$ | C. | (-2,1),2 | D. | (2,-1),2 |
17.已知α是第二象限角,sinα=$\frac{5}{13}$,则cosα=( )
| A. | -$\frac{5}{13}$ | B. | -$\frac{12}{13}$ | C. | $\frac{5}{13}$ | D. | $\frac{12}{13}$ |
18.将正方形的每条边8等分,再取分点为顶点(不包括正方形的顶点),可以得到不同的三角形个数为( )
| A. | 1372 | B. | 2024 | C. | 3136 | D. | 4495 |
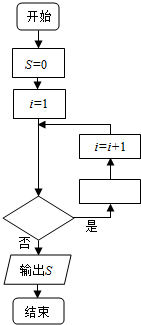 如图是计算1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2015}$的值的程序框图.
如图是计算1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2015}$的值的程序框图.