题目内容
7.化简:$\frac{cos(π+α)ta{n}^{2}(2π-α)cos(α-3π)}{sin(π-α)sin(2π-α)}$.分析 由条件利用诱导公式、同角三角函数的基本关系,化简所给式子的值,可得结果.
解答 解:$\frac{cos(π+α)ta{n}^{2}(2π-α)cos(α-3π)}{sin(π-α)sin(2π-α)}$=$\frac{-cosα{•tan}^{2}α•(-cosα)}{sinα•(-sinα)}$=$\frac{{sin}^{2}α}{{-sin}^{2}α}$=-1.
点评 本题主要考查同角三角函数的基本关系,应用诱导公式化简三角函数式,要特别注意符号的选取,这是解题的易错点,属于基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
18.函数y=x-sinx,x∈[$\frac{π}{2}$,π]的最大值是( )
| A. | $\frac{π}{2}-1$ | B. | π-1 | C. | π | D. | π+1 |
12.复数$1+\frac{5}{2-i}$(i是虚数单位)的模等于( )
| A. | $\sqrt{10}$ | B. | 10 | C. | $\sqrt{5}$ | D. | 5 |
19.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x≤1}\\{lo{g}_{3}(x-1),x>1}\end{array}\right.$,且f(x0)=1,则x0=( )
| A. | 0 | B. | 4 | C. | 0或4 | D. | 1或3 |
17.已知α是第二象限角,sinα=$\frac{5}{13}$,则cosα=( )
| A. | -$\frac{5}{13}$ | B. | -$\frac{12}{13}$ | C. | $\frac{5}{13}$ | D. | $\frac{12}{13}$ |
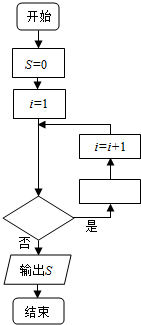 如图是计算1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2015}$的值的程序框图.
如图是计算1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2015}$的值的程序框图.