题目内容
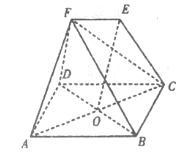
【题目】如图,在直三棱柱ABC﹣A1B1C1中,点D、E、F分别为线段A1C1、AB、A1A的中点,A1A=AC=BC,∠ACB=90°.求证:

(1)DE∥平面BCC1B1;
(2)EF⊥平面B1CE.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)取B1C1的中点M,连接D1M,BM,证明四边形DMBE是平行四边形,得到证明.
(2)根据勾股定理得EF⊥CE,根据三角函数关系得到EF⊥B1E,得到证明.
(1)如图所示:取B1C1的中点M,连接D1M,BM,由题意得DM∥A1B1,
∴DM∥AB,且DM是△A1B1C1的中位线,DM![]() AB=BE,
AB=BE,
所以四边形DMBE是平行四边形,
∴DE∥BM,又DE面BCC1B1,BM面BCC1B1
∴DE∥平面BCC1B1.
(2)由题意设AC=2,则AB=2![]() ,AE
,AE![]() ,AF=1,
,AF=1,
在△AEF中,EF![]() ,
,
而CE![]() AB
AB![]() ,Rt△ACF中,CF
,Rt△ACF中,CF![]() ,
,
∴△CEF中CE2+EF2=CF2,由勾股定理得,EF⊥CE,
tan∠FEC![]() ,tan∠BEB1
,tan∠BEB1![]() ,所以tan∠FECtan∠BEB1=1,
,所以tan∠FECtan∠BEB1=1,
所以EF⊥B1E,又CE∩EB1=E,CE平面B1CE,B1E平面B1CE,
∴EF⊥平面B1CE.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目