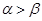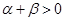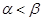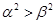题目内容
函数f(x)=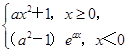 在(-∞,+∞)上单调,则a的取值范围是________.
在(-∞,+∞)上单调,则a的取值范围是________.
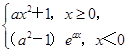 在(-∞,+∞)上单调,则a的取值范围是________.
在(-∞,+∞)上单调,则a的取值范围是________.(-∞,-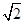 ]∪(1,
]∪(1,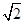 ]
]
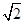 ]∪(1,
]∪(1,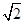 ]
]若a>0,则f(x)=ax2+1在[0,+∞)上单调增,
∴f(x)=(a2-1)eax在(-∞,0)上单调增,
∴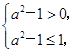 ∴1<a≤
∴1<a≤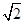 .同理,当a<0时,可求得a≤-
.同理,当a<0时,可求得a≤-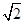 ,故a∈(-∞,-
,故a∈(-∞,-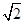 ]∪(1,
]∪(1,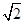 ]
]
∴f(x)=(a2-1)eax在(-∞,0)上单调增,
∴
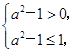 ∴1<a≤
∴1<a≤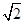 .同理,当a<0时,可求得a≤-
.同理,当a<0时,可求得a≤-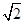 ,故a∈(-∞,-
,故a∈(-∞,-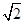 ]∪(1,
]∪(1,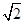 ]
]
练习册系列答案
相关题目
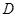 上的函数
上的函数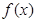 ,如果满足:对任意
,如果满足:对任意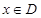 ,存在常数
,存在常数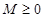 ,都有
,都有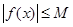 成立,则称
成立,则称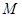 称为函数
称为函数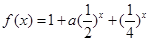 ,
,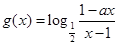 .
.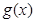 为奇函数,求实数
为奇函数,求实数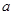 的值;
的值;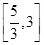 上的所有上界构成的集合;
上的所有上界构成的集合;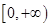 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数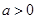 且
且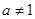 ,函数
,函数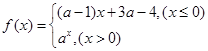 满足对任意实数
满足对任意实数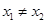 ,都有
,都有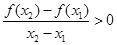 成立,则
成立,则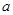 的取值范围是 ( )
的取值范围是 ( )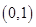
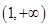 (
(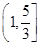 (
(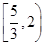
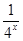 -
-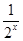 +1的最小值与最大值.
+1的最小值与最大值.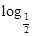 a)≤2f(1),则a的取值范围是________.
a)≤2f(1),则a的取值范围是________.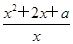 ,x∈[1,+∞).
,x∈[1,+∞).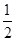 时,求f(x)的最小值;
时,求f(x)的最小值;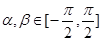 且
且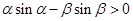 ,则下面结论正确的是( )
,则下面结论正确的是( )