题目内容
19. 设函数f(x)=|x2-2x-3|.
设函数f(x)=|x2-2x-3|.(1)求函数f(x)的零点
(2)在给出的平面直角坐标系中直接画出函数f(x)的图象,并写出单调区间.
分析 (1)f(x)=|x2-2x-3|=0,可得函数f(x)的零点;
(2)去掉绝对值,原函数变成:f(x)=|x2-2x-3|=$\left\{\begin{array}{l}{-{x}^{2}+2x+3=-(x-1)^{2}+4,-1≤x≤3}\\{{x}^{2}-2x-3=(x-1)^{2}-4,x<-1或x>3}\end{array}\right.$,画出每段上的二次函数图象,根据图象即可写出单调区间.
解答 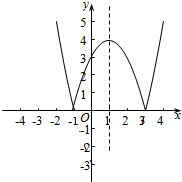 解:(1)f(x)=|x2-2x-3|=0,∴x=-1或3.
解:(1)f(x)=|x2-2x-3|=0,∴x=-1或3.
(2)f(x)=|x2-2x-3|=$\left\{\begin{array}{l}{-{x}^{2}+2x+3=-(x-1)^{2}+4,-1≤x≤3}\\{{x}^{2}-2x-3=(x-1)^{2}-4,x<-1或x>3}\end{array}\right.$.
∴图象为:
通过图象可以看出单调增区间为:[-1,1],(3,+∞);单调减区间为:(-∞,-1),(1,3].
点评 本题主要考查含绝对值函数图象的画法及通过图形求单调区间的方法,属于中档题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
11.某电子广告牌连续播出四个广告,假设每个广告所需的时间互相独立,且都是整数分钟,经统计,以往播出100次所需的时间(t)的情况如下:
每次随机播出,若将频率视为概率.
(Ⅰ)求恰好在开播第6分钟后开始播出第3号广告的概率;
(Ⅱ)求第4分钟末完整播出广告1次的概率.
| 类别 | 1号广告 | 2号广告 | 3号广告 | 4号广告 |
| 广告次数 | 20 | 30 | 40 | 10 |
| 时间t(分钟/人) | 2 | 3 | 4 | 6 |
(Ⅰ)求恰好在开播第6分钟后开始播出第3号广告的概率;
(Ⅱ)求第4分钟末完整播出广告1次的概率.
4.点P(x0,y0)在直线l:f(x,y)=0外,则l1:f(x,y)+f(x0,y0)=0与l2:f(-y,x)+f(x0,y0)=0的位置关系是( )
| A. | 平行 | B. | 垂直 | C. | 平行或重合 | D. | 相交且不垂直 |
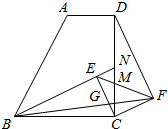 在四边形ABCD中,AD∥BC,BC=CD,∠ADC=90°,BC=DC=2AD,E为四边形ABCD内一点,F为四边形ABCD外一点,且∠BEC=∠DFC=90°,BE∥CF交CD的中点于N.
在四边形ABCD中,AD∥BC,BC=CD,∠ADC=90°,BC=DC=2AD,E为四边形ABCD内一点,F为四边形ABCD外一点,且∠BEC=∠DFC=90°,BE∥CF交CD的中点于N. 和
和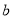 两数之间插入5个数,使他们与
两数之间插入5个数,使他们与 组成等差数列,则该数列的公差为( )
组成等差数列,则该数列的公差为( )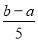 B.
B. C.
C.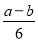 D.
D.
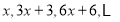 的第四项等于( )
的第四项等于( )