题目内容
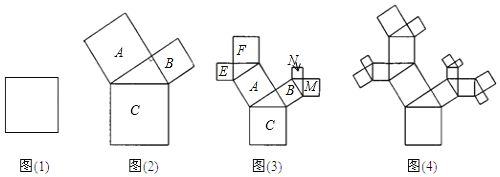
【题目】图一是美丽的“勾股树”,它是一个直角三角形分别以它的每一边向外作正方形而得到.图二是第1代“勾股树”,重复图二的作法,得到图三为第2代“勾股树”,以此类推,已知最大的正方形面积为1,则第![]() 代“勾股树”所有正方形的个数与面积的和分别为( )
代“勾股树”所有正方形的个数与面积的和分别为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
第1代“勾股树”中,小正方形的个数3=21+1﹣1=3,所有正方形的面积之和为2=(1+1)×1,第2代“勾股树”中,小正方形的个数7=22+1﹣1,所有的正方形的面积之和为3=(2+1)×1,以此类推,第n代“勾股树”所有正方形的个数为2n+1﹣1,第n代“勾股树”所有正方形的面积的和为:(n+1)×1=n+1.
解:第1代“勾股树”中,小正方形的个数3=21+1﹣1=3,
如图(2),设直角三角形的三条边长分别为a,b,c,
根据勾股定理得a2+b2=c2,
即正方形A的面积+正方形B的面积=正方形C的面积=1,
所有正方形的面积之和为2=(1+1)×1,
第2代“勾股树”中,小正方形的个数7=22+1﹣1,
如图(3),正方形E的面积+正方形F的面积=正方形A的面积,
正方形M的面积+正方形N的面积=正方形B的面积,
正方形E的面积+正方形F的面积+正方形M的面积+正方形N的面积=正方形A的面积+正方形B的面积=正方形C的面积=1,
所有的正方形的面积之和为3=(2+1)×1,
…
以此类推,第n代“勾股树”所有正方形的个数为2n+1﹣1,
第n代“勾股树”所有正方形的面积的和为:(n+1)×1=n+1.
故选:A.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



