题目内容
【题目】已知数列![]() 满足
满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求
,求![]() ;
;
(3)设![]() ,问:是否存在非零整数
,问:是否存在非零整数![]() ,使数列
,使数列![]() 为递增数列?若存在,求出
为递增数列?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]()
(2)![]()
(3)存在,![]()
【解析】
(1)根据题干中的等式即可求解数列![]() 的通项公式;
的通项公式;
(2)先根据数列![]() 的通项公式求出
的通项公式求出![]() ,再根据
,再根据![]() 的特点利用错位相减法求和即可;
的特点利用错位相减法求和即可;
(3)先求出![]() ,再分
,再分![]() 为奇数和
为奇数和![]() 为偶数两种情况求解即可.
为偶数两种情况求解即可.
(1)由题意,数列![]() 满足
满足![]() ……①,
……①,
所以当![]() 时,
时,![]() …… ②,
…… ②,
由①-②,可得![]() ,可得
,可得![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() ,也满足上式,
,也满足上式,
所以![]() .
.
(2)由(1)知,![]() ,
,
则![]() ,
,
![]() ,
,
两式相减得,![]() ,
,
所以![]() .
.
(3)由(1)知,![]() ,要使数列
,要使数列![]() 为递增数列,
为递增数列,
则![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立,
整理得![]() 恒成立,所以
恒成立,所以![]() 恒成立.
恒成立.
当![]() 为奇数时,
为奇数时,![]() 恒成立,所以
恒成立,所以![]() ;
;
当![]() 为偶数时,
为偶数时,![]() 恒成立,所以
恒成立,所以![]() .
.
综上可得![]() ,
,
又因为![]() 为非零整数,所以
为非零整数,所以![]() ,
,
即存在![]() ,使数列
,使数列![]() 为递增数列.
为递增数列.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了解某初中学校学生睡眠状况,在该校全体学生中随机抽取了容量为120的样本,统计睡眠时间(单位:![]() ).经统计,时间均在区间
).经统计,时间均在区间![]() 内,将其按
内,将其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
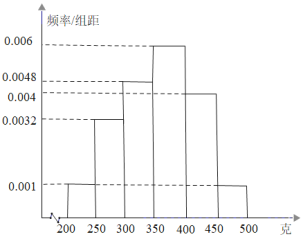
,![]() 分成6组,制成如图所示的频率分布直方图:
分成6组,制成如图所示的频率分布直方图:

(1)世界卫生组织表明,该年龄段的学生睡眠时间![]() 服从正态分布
服从正态分布![]() ,其标准为:该年龄段的学生睡眠时间的平均值
,其标准为:该年龄段的学生睡眠时间的平均值![]() ,方差
,方差![]() .根据
.根据![]() 原则,用样本估计总体,判断该初中学校学生睡眠时间在区间
原则,用样本估计总体,判断该初中学校学生睡眠时间在区间![]() 上是否达标?
上是否达标?
(参考公式:![]() ,
,![]() ,
,![]() )
)
(2)若规定睡眠时间不低于![]() 为优质睡眠.已知所抽取的这120名学生中,男、女睡眠质量人数如下
为优质睡眠.已知所抽取的这120名学生中,男、女睡眠质量人数如下![]() 列联表所示:
列联表所示:
优质睡眠 | 非优质睡眠 | 合计 | |
男 | 60 | ||
女 | 19 | ||
合计 |
将列联表数据补充完整,并判断是否有![]() 的把握认为优质睡眠与性别有关系,并说明理由;
的把握认为优质睡眠与性别有关系,并说明理由;
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: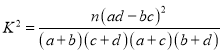 ,其中
,其中![]() .)
.)