题目内容
【题目】已知平行四边形ABCD中.∠BAD=120°,AB=1,AD=2,点P是线段BC上的一个动点,则 ![]()
![]() 的取值范围是 .
的取值范围是 .
【答案】[﹣ ![]() ,2]
,2]
【解析】解:以B为坐标原点,以BC所在的直线为x轴,建立如图所述的直角坐标系,作AE⊥BC, 垂足为E,
∵∠BAD=120°,AB=1,AD=2,
∴∠ABC=60°,
∴AE= ![]() ,BE=
,BE= ![]() ,
,
∴A( ![]() ,
, ![]() ),D(
),D( ![]() ,
, ![]() ),
),
∵点P是线段BC上的一个动点,设点P(x,0),0≤x≤2,
∴ ![]() =(x﹣
=(x﹣ ![]() ,﹣
,﹣ ![]() ),
), ![]() =(x﹣
=(x﹣ ![]() ,﹣
,﹣ ![]() ),
),
∴ ![]()
![]() =(x﹣
=(x﹣ ![]() )(x﹣
)(x﹣ ![]() )+
)+ ![]() =(x﹣
=(x﹣ ![]() )2﹣
)2﹣ ![]() ,
,
∴当x= ![]() 时,有最小值,最小值为﹣
时,有最小值,最小值为﹣ ![]() ,
,
当x=0时,有最大值,最大值为2,
则 ![]()
![]() 的取值范围为[﹣
的取值范围为[﹣ ![]() ,2],
,2],
所以答案是:[﹣ ![]() ,2].
,2].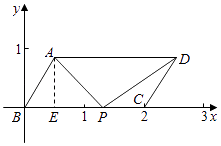

练习册系列答案
相关题目
【题目】某产品的广告费用x与销售额y的统计数据如表:
广告费用x(万元) | 1 | 2 | 4 | 5 |
销售额y(万元) | 6 | 14 | 28 | 32 |
根据上表中的数据可以求得线性回归方程 ![]() =
= ![]() x+
x+ ![]() 中的
中的 ![]() 为6.6,据此模型预报广告费用为10万元时销售额为( )
为6.6,据此模型预报广告费用为10万元时销售额为( )
A.66.2万元
B.66.4万元
C.66.8万元
D.67.6万元